Mesurer la variabilité avec l’étendu ou plage ou fourchette ou gamme
Tout comme il existe trois façons principales de mesurer la tendance centrale dans une distribution de fréquence, il existe plusieurs façons de mesurer la variabilité. Deux de ces méthodes, l’écart type et la variance, sont étroitement liées et
occupent la plus grande partie de la discussion dans ce chapitre.
Une troisième façon de mesurer la variabilité est l’étendu ou plage ou gamme ou fourchette : la valeur maximale dans un ensemble moins la valeur minimale. Il est généralement utile de connaître la plage des valeurs dans une distribution de fréquence, ne serait-ce que pour se prémunir contre les erreurs dans la saisie des données. Par exemple, supposons que vous ayez une liste dans une feuille de calcul Excel contenant les températures corporelles, mesurées en Fahrenheit, de 100 hommes. Si la plage calculée, la température maximale moins la température minimale, est de 888 degrés, vous savez assez rapidement que quelqu’un a laissé tomber un point décimal quelque part. Peut-être que vous avez entré 986 au lieu de 98,6.
Remarque
Historiquement, en particulier dans le domaine du contrôle statistique des processus (une technique utilisée dans la gestion de la qualité dans la fabrication), certains praticiens bien connus ont préféré la fourchette comme estimation de la variabilité. Ils prétendent, avec une certaine justification, qu’une statistique telle que l’écart type est influencée à la fois par la nature sous-jacente d’un système de fabrication et par des événements spéciaux tels que des erreurs humaines qui font qu’un système échappe à tout contrôle. En revanche, la plage est « robuste ».
Il est vrai que l’écart-type prend en compte toutes les valeurs dans le calcul de la variabilité globale d’un ensemble de nombres, et certaines de ces valeurs sont des valeurs aberrantes normales – des failles rouges qui n’appellent pas vraiment d’investigation supplémentaire. Mais il ne s’ensuit pas nécessairement que la plage est sensible uniquement aux problèmes occasionnels, tels que les erreurs humaines, qui nécessitent une détection et une correction.
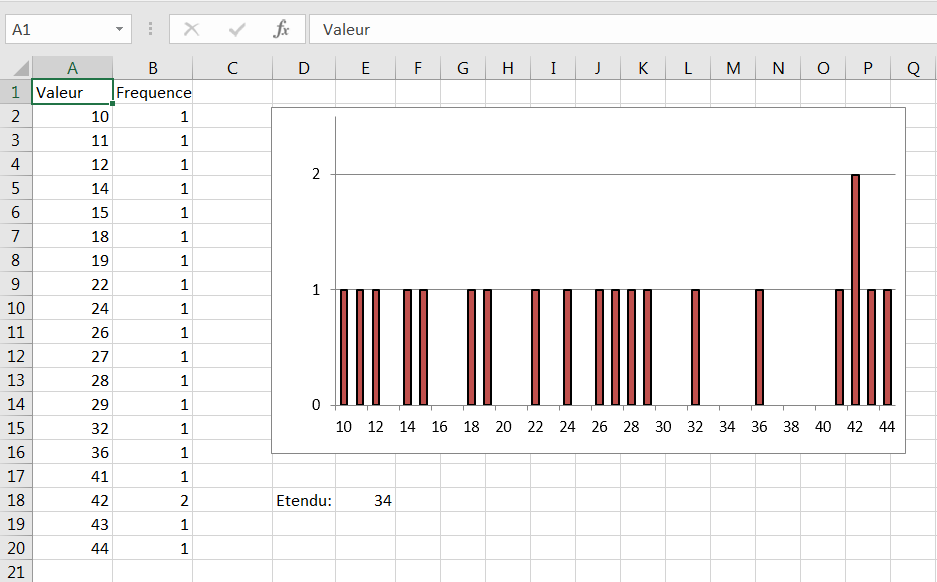
L’utilisation de la plage comme unique mesure de la variabilité dans un ensemble de données présente certains inconvénients, mais c’est une bonne idée de la calculer de toute façon pour mieux comprendre la nature de vos données. Par exemple, la figure 3.1 montre une distribution de fréquence qui peut être raisonnablement décrite en partie en utilisant la plage.
Figure 3.1. La distribution est approximativement symétrique et la plage est un descripteur utile.
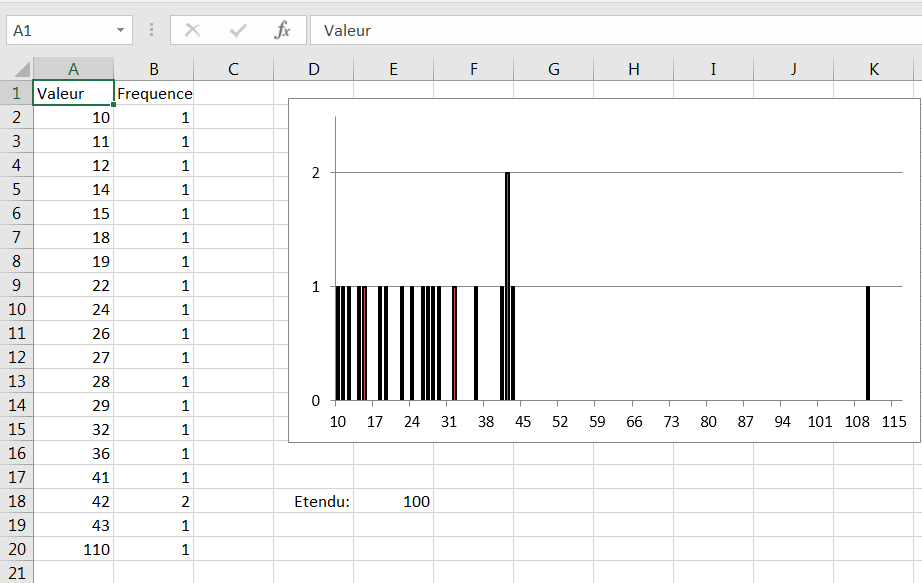
Comme un nombre appréciable d’observations apparaissent à chaque extrémité de la distribution, il est utile de savoir que la fourchette que les valeurs occupent est de 34. La figure 3.2 présente une image différente. Il suffit d’une valeur extrême pour que la plage présente une image trompeuse du degré de variabilité dans un ensemble de données. La fourchette calculée à la figure 3.2 représente environ trois fois la taille de la fourchette de la figure 3.1. En revanche, l’écart type (examiné dans la section suivante) de la figure 3.2 est environ deux fois plus grand que l’écart-type de la figure 3.1. C’est un jugement subjectif, bien sûr, mais avec ces données, je considère l’écart type comme la mesure la plus précise du degré de variabilité dans l’échantillon. (Les parcelles à boîte et à moustaches, examinées au chapitre 5, sont particulièrement utiles dans ce genre de situation.)
Figure 3.2. La valeur solitaire en haut de la distribution crée une estimation de plage qui décrit mal la nature de la distribution.