■■ Qu’est-ce que cela signifie lorsque nous disons qu’une variable indépendante a un effet non linéaire sur une variable dépendante?

■■ Qu’est-ce que cela signifie lorsque nous disons que les effets de deux variables indépendantes sur une variable dépendante interagissent?

■■ Comment puis-je tester la présence de non-linéarité et d’interaction dans une régression?

Réponses aux questions de cet article

Cette section fournit les réponses aux questions répertoriées au début de cet article.

Qu’est-ce que cela signifie lorsque nous disons qu’une variable indépendante a un effet non linéaire sur une variable dépendante?

Une variable indépendante influence souvent une variable dépendante via une relation non linéaire. Par exemple, si vous essayez de prédire les ventes de produits en utilisant une équation telle que Sales = 500 – 10 * Price, le prix influence les ventes de façon linéaire. Cette équation indique qu’une augmentation unitaire du prix (à n’importe quel niveau de prix) réduira les ventes de 10 unités. Si la relation entre les ventes et le prix était régie par une équation telle que Ventes = 500 + 4 * Prix – .40 * Prix2, le prix et les ventes seraient liés de manière non linéaire. Comme montré

dans la figure 1, des augmentations de prix plus importantes entraînent une baisse plus importante de la demande (voir la feuille de travail Non-linéarité du fichier ). En bref, si le changement dans la variable dépendante provoqué par un changement d’unité dans la variable indépendante n’est pas constant, il existe une relation non linéaire entre les variables indépendantes et dépendantes.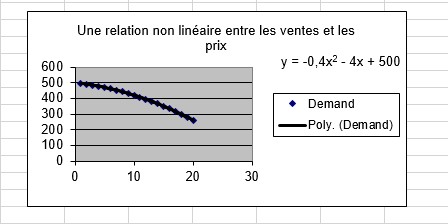

FIGURE 1 Cette figure montre une relation non linéaire entre la demande et le prix.

Qu’est-ce que cela signifie lorsque nous disons que les effets de deux variables indépendantes sur une variable dépendante interagissent?

Si l’effet d’une variable indépendante sur une variable dépendante dépend de la valeur d’une autre variable indépendante, vous pouvez dire que les deux variables indépendantes présentent une interaction. Par exemple, supposons que vous essayez de prédire les ventes en utilisant le prix et le montant dépensé en publicité. Si l’effet du changement du niveau des dollars publicitaires est important lorsque le prix est petit et petit lorsque le prix est élevé, le prix et la publicité présentent une interaction. Si l’effet du changement du niveau des dollars publicitaires est le même pour n’importe quel niveau de prix, les ventes et le prix ne présentent aucune interaction.

Comment puis-je tester la présence de non-linéarité et d’interaction dans une régression?

Pour voir si une variable indépendante a un effet non linéaire sur une variable dépendante, vous ajoutez simplement une variable indépendante à la régression qui est égale au carré de la variable indépendante. Si le terme au carré a une faible valeur p (inférieure à 0,15), vous avez la preuve d’une relation non linéaire.

Pour vérifier si deux variables indépendantes présentent une interaction, ajoutez un terme à la régression qui est égal au produit des variables indépendantes. Si le terme a une faible valeur p (inférieure à 0,15), vous avez des preuves d’interaction. Pour illustrer cela, essayez de déterminer comment le sexe et l’expérience influencent les salaires dans une petite entreprise manufacturière. Pour chaque employé, vous recevez l’ensemble de données suivant. Vous pouvez trouver les informations dans la feuille de calcul Data du fichier, illustré à la figure 2:

■■ Salaire annuel (en milliers de dollars)

■■ Années d’expérience dans le secteur manufacturier

■■ Sexe (1 = femme, 0 = homme)

Utilisez ces données pour prédire le salaire (la variable dépendante) en fonction des années d’expérience et du sexe. Pour vérifier si les années d’expérience ont un effet non linéaire sur le salaire, ajoutez le terme Expérience au carré en copiant la formule B2² de D2 à D3: D98. Pour tester si l’expérience et le sexe ont une interaction significative, ajoutez le terme Expérience * Sexe en copiant la formule B2 * C2 à partir de E2 à E3: E98. Exécutez une régression avec une plage d’entrée Y de A1: A98 et une plage d’entrée X de B1: E98. Après avoir sélectionné Étiquettes dans la boîte de dialogue Régression et cliqué sur OK, vous devriez obtenir les résultats illustrés à la figure 3.

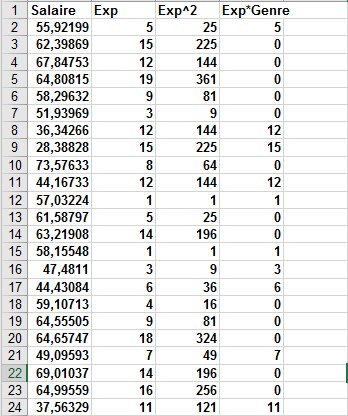
FIGURE 2 Il s’agit des données permettant de prévoir le salaire en fonction du sexe et de l’expérience.

Vous pouvez voir que le sexe est insignifiant (sa valeur de p est supérieure à 0,15). Toutes les autres variables indépendantes sont significatives (ce qui signifie qu’elles ont une valeur de p inférieure ou égale à 0,15). Vous pouvez supprimer la variable de genre non significative en tant que variable indépendante. Pour ce faire, copiez les données dans une nouvelle feuille de calcul appelée FinalRegression. (Cliquez avec le bouton droit sur n’importe quel onglet de feuille de calcul, cliquez sur Déplacer ou copier, puis activez la case à cocher Créer une copie.) Après avoir supprimé la colonne Sexe, vous obtenez les résultats de la régression inclus dans la feuille de calcul FinalRegression et illustrés à la figure 4.

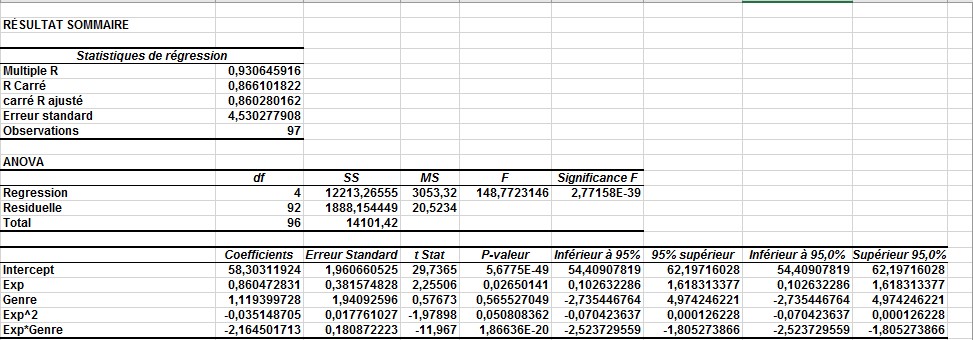
FIGURE 3 Ce sont des résultats de régression qui testent la non-linéarité et l’interaction.

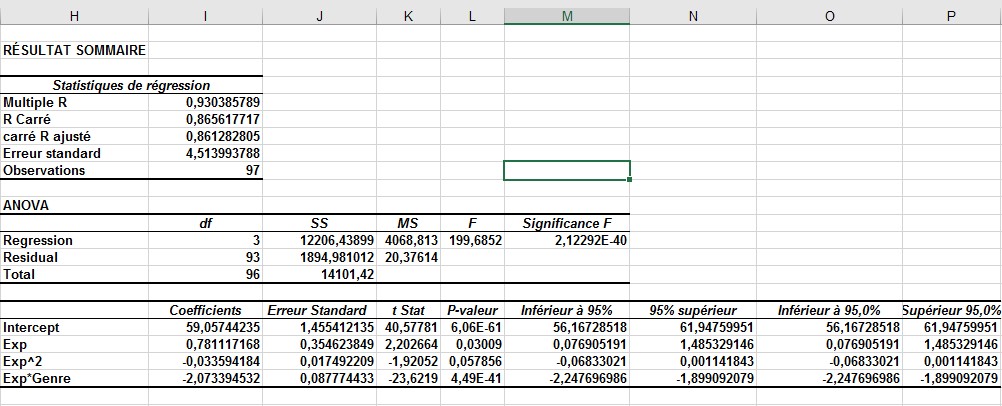
FIGURE 4 Voici les résultats de la régression après la suppression de la variable de sexe insignifiante.

Toutes les variables indépendantes sont désormais significatives (ont une valeur de p inférieure ou égale à 0,15). Par conséquent, vous pouvez prédire le salaire (en milliers de dollars) en utilisant l’équation suivante (equation   n 1):

Salaire prévu = 59,06 + 0,78 (EXP) -. 033EXP2-2,07 (EXP * GENRE)

Le terme EXP2 négatif indique que chaque année supplémentaire d’expérience a moins d’impact sur le salaire, ce qui signifie que l’expérience a un effet non linéaire sur le salaire. En fait, ce modèle montre qu’après 13 ans d’expérience, chaque année supplémentaire d’expérience réduit réellement le salaire.

N’oubliez pas que le sexe est égal à 1 pour une femme et à 0 pour un homme. Après avoir substitué 1 au sexe dans l’équation 1, le salaire d’une femme peut être prédit comme suit:

Salaire prévu = 59,06 + 78EXP-.033EXP2 –2,07 (EXP * 1) = 59,06-.033EXP2–1,29EXP

Pour un homme (en substituant le genre = 0), l’équation suivante peut être utilisée:

Salaire prévu = 59,06 + .78EXP-.033EXP2 –2.07 (EXP * 0) = 59.06 + .78EXP-.033EXP2

Ainsi, l’interaction entre le sexe et l’expérience montre que chaque année supplémentaire d’expérience profite à une femme en moyenne 0,78 – (–1,29) = 2 070 $ de moins qu’un homme. Cela indique que les femmes ne sont pas traitées équitablement.