Obtenir les valeurs prévues
Si vous n’avez qu’une seule valeur new_x à prédire, vous pouvez entrer la formule avec la fonction TENDANCE () simplement en la tapant et en appuyant sur Entrée. C’est la situation de la figure 4.15

, où vous devez entrer = TENDANCE (C2: C11, B2: B11, B18) dans une cellule vide telle que C18 pour obtenir le poids prévu compte tenu de la Taille dans B18.
Mais supposons que vous vouliez savoir quel serait le poids prévu de tous les sujets de votre échantillon, étant donné la corrélation entre les deux variables. TENDANCE () le fait aussi pour vous: vous avez simplement besoin d’entrer dans la table.
Vous commencez par sélectionner une plage de cellules ayant les mêmes dimensions que celles de votre fichier known_x. Dans la figure 4.15, les x connus sont dans B2: B11, vous pouvez donc sélectionner D2: D11. Tapez ensuite la formule = TENDANCE (C2: C11, B2: B11) et ensuite Ctrl + Shift + Entrer au lieu de simplement entrer.

Remarque
Les formules de tableau sont discutées plus en détail dans le chapitre 2, dans la section intitulée «Utilisation d’une formule de tableau pour compter les valeurs».
Le résultat apparaît sur la Figure 4.16.
Figure 4.16. Les accolades autour de la formule dans la boîte de formule indiquent qu’il s’agit d’une formule matricielle.

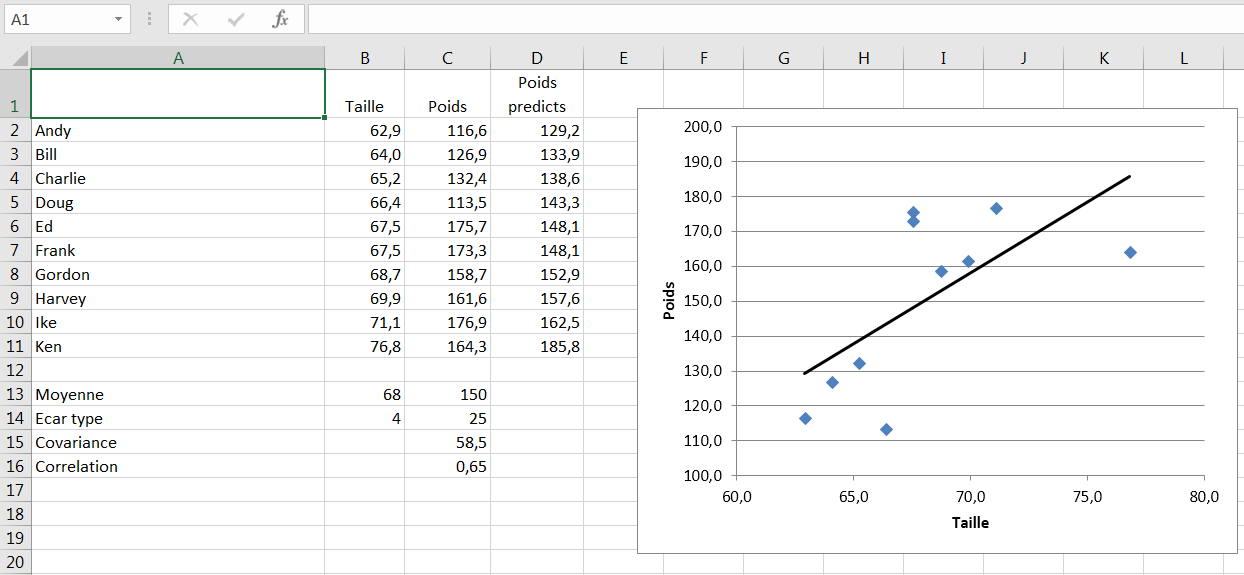
Vous pouvez mieux comprendre la signification de la courbe de tendance dans le graphique si vous utilisez les valeurs prédites dans D2: D11 de la Figure 4.16. Si vous créez un graphique XY en utilisant les valeurs de B2: B11 et D2: D11, vous verrez que vous avez un graphique qui duplique la courbe de tendance dans le graphique de la figure 4.16.
Ainsi, une ligne de tendance linéaire dans un graphique représente la situation irréaliste dans laquelle toutes les observations suivent docilement une formule qui relie deux variables. Mais Ed mange trop et Doug ne mange pas assez. Ils s’éloignent dans une certaine mesure de la ligne de tendance parfaite.
Si c’est irréaliste, à quoi sert d’inclure une ligne de tendance dans un graphique ? Il s’agit en grande partie de vous aider à visualiser à quel point les observations individuelles tombent de la formule mathématique. Plus les écarts sont importants, plus la corrélation est faible.

Obtenir la formule de régression
Une section précédente de ce chapitre, «Suppression des effets de l’échelle», a expliqué comment utiliser les scores z, les moyennes et les écarts-types et le coefficient de corrélation pour prédire une variable par rapport à une autre. La section suivante, “Utilisation de la fonction Excel”, décrit comment utiliser la fonction TENDANCE () pour passer directement des valeurs observées aux valeurs prédites.
Aucune discussion n’a traité de la formule que vous pouvez utiliser sur les données brutes. Il est possible d’utiliser deux fonctions Excel, PENTE () et ORDONNEE.ORIGINE (), pour générer la formule qui renvoie les valeurs prédites que vous obtenez avec TENDANCE ().
Une formule qui décrit le mieux la relation entre deux variables, comme la taille et le poids des figures 4.14 à 4.16, nécessite deux nombres: une pente et une ordonnée à l’origine. La pente fait référence à la pente de la droite de régression. La pente indique le nombre d’unités que la ligne déplace vers le haut pour chaque unité que la ligne déplace à droite. La pente peut être positive ou négative: si elle est positive, la droite de régression descend du coin inférieur gauche vers le coin supérieur droit, comme dans la figure 4.16: si elle est négative, la pente va du coin supérieur gauche au coin inférieur droit.

Vous calculez la valeur de la pente directement dans Excel avec la fonction PENTE (). Par exemple, en utilisant les données des Figures 4.14 à 4.16, la valeur renvoyée par la formule
= PENTE (C2: C11, B2: B11)
et qui nous donne 4,06. C’est-à-dire, pour chaque unité d’augmentation (chaque pouce) de hauteur dans cet échantillon, vous vous attendez à un peu plus de quatre livres d’augmentation de poids.
Mais la pente n’est pas tout ce dont vous avez besoin: vous avez aussi besoin de ce qu’on appelle l’interception. C’est la valeur de la variable prédite – ici, poids – au point que la droite de régression croise son axe. Dans la figure 4.17, la ligne de régression a été étendue vers la gauche, vers le point zéro sur l’axe horizontal où elle croise l’axe vertical. Le point où la droite de régression traverse l’axe vertical est la valeur de l’interception.
Figure 4.17. Les plages de valeurs sur les axes ont été augmentées afin de montrer l’interception.

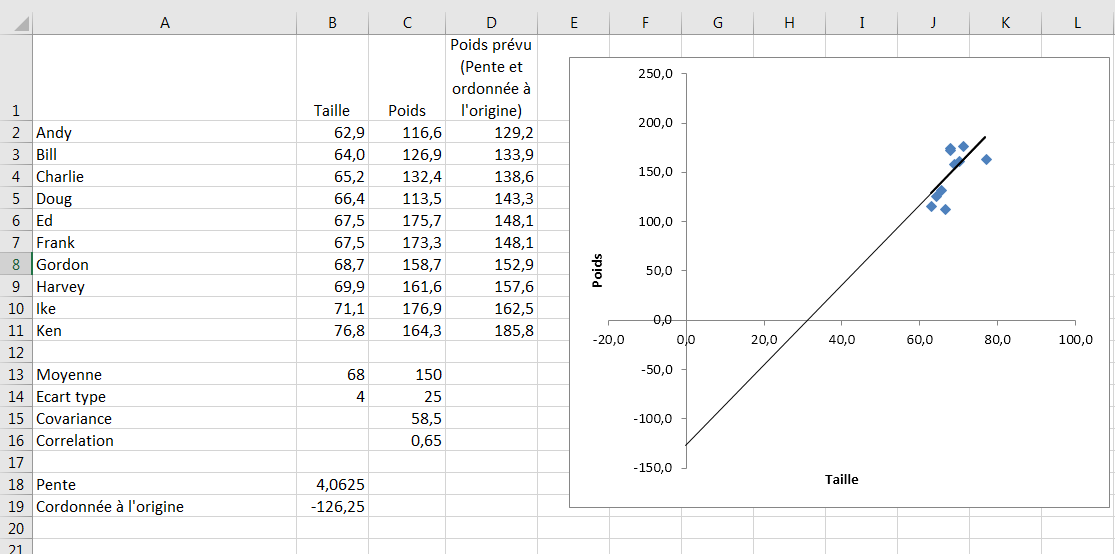
Les valeurs de la pente et de l’ordonnée à l’origine de la droite de régression sont indiquées dans B18 et B19 de la figure 4.17. Notez que la valeur d’interception affichée dans la cellule B19 correspond au point dans le graphique où la ligne de régression croise l’axe vertical.
Les valeurs prédites pour le poids sont indiquées dans les cellules D2: D11 de la figure 4.17.