■■ Comment puis-je déterminer si des facteurs spécifiques influencent le trafic client?

■■ Comment puis-je évaluer l’exactitude des prévisions?

■■ Comment puis-je vérifier si mes erreurs de prévision sont aléatoires?

Pour un projet étudiant au début des années 90 (avant le dépôt direct!), Une classe et moi avons tenté de prévoir le nombre de clients visitant chaque jour la succursale Eastland Plaza de la coopérative de crédit de l’Université de l’Indiana (IU). Les entretiens avec le directeur d’agence ont clairement montré que les facteurs suivants affectaient le nombre de clients:

■■ Mois de l’année

■■ Jour de la semaine

■■ Si la journée était un jour de paie pour le corps professoral ou le personnel

■■ Que la veille ou le lendemain soit un jour férié

Réponses aux questions de ce article

Cette section fournit les réponses aux questions répertoriées au début de cet article.

Comment puis-je déterminer si des facteurs spécifiques influencent le trafic client?

Les données collectées sont contenues dans la feuille de calcul d’origine dans le fichier , illustré à la figure-1. Si vous essayez d’exécuter une régression sur ces données à l’aide de variables fictives (comme décrit dans l’article 58, «Incorporation de facteurs qualitatifs dans la régression multiple»), la variable dépendante serait le nombre de clients arrivant chaque jour (les données de la colonne E). Vous auriez besoin de 19 variables indépendantes:

■■ Onze pour représenter le mois (12 mois moins 1)

■■ Quatre pour tenir compte du jour de la semaine (5 jours ouvrables moins 1)

■■ Deux pour tenir compte des types de jours de paie qui se produisent chaque mois

■■ Deux pour tenir compte du fait qu’un jour particulier suit ou précède un jour férié

Microsoft Excel  n’autorise que 15 variables indépendantes, il semble donc que vous ayez des problèmes.

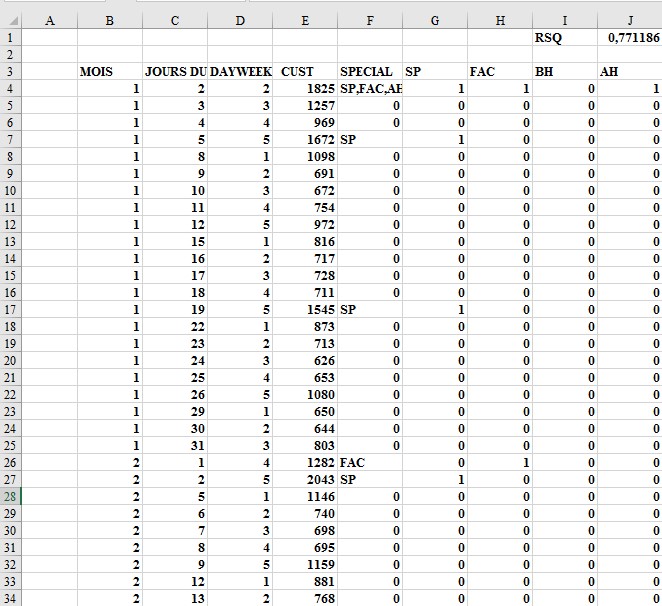
FIGURE 1 Données utilisées pour prédire le trafic client des coopératives de crédit.

Lorsqu’un modèle de prévision de régression nécessite plus de 15 variables indépendantes, vous pouvez utiliser le solveur Excel pour estimer les coefficients des variables indépendantes. Vous pouvez également utiliser Excel pour calculer les valeurs R au carré entre les prévisions et le trafic client réel et l’écart type pour les erreurs de prévision. Pour analyser ces données (voir la figure 65-2), une équation de prévision a été créée à l’aide d’une table de recherche pour localiser le jour de la semaine, le mois et d’autres facteurs. Alors solveur a été utilisé pour choisir les coefficients pour chaque niveau de chaque facteur qui donne la somme minimale des erreurs quadratiques. (L’erreur de chaque jour est égale aux clients réels moins les clients prévus.) Voici les détails.

Commencez par créer des variables indicatrices (dans les colonnes G à J) pour savoir si le jour est un jour de paie du personnel (SP), un jour de paie du corps professoral (FAC), avant un jour férié (BH) ou après un jour férié (AH). (Voir la figure 65-1.) Par exemple, dans les cellules G4, H4 et J4, entrez 1 pour indiquer que le 2 janvier était un jour de paie du personnel, un jour de paie de la faculté et après un jour férié. La cellule I4 contient 0 pour indiquer que le 2 janvier n’était pas avant un jour férié.

La prévision est définie par une constante (qui permet de centrer les prévisions afin qu’elles soient plus précises) et des effets pour chaque jour de la semaine, chaque mois, un jour de paie du personnel, un jour de paie de la faculté, un jour avant les vacances et un jour survenant après un jour férié. Insérez des valeurs d’essai pour tous ces paramètres (les cellules changeantes du solveur) dans la plage de cellules O4: O26, comme illustré à la figure 2. Le solveur choisira alors valeurs qui rendent le modèle le mieux adapté aux données. Pour chaque jour, la prévision du nombre de clients sera généré par l’équation suivante:

Nombre de clients prévu = Constante + (effet Mois) + (effet Jour de la semaine)

+ (Effet sur salaire du personnel, le cas échéant) + (Effet sur salaire de la faculté, le cas échéant) +

(Avant effet vacances, le cas échéant) + (Après effet vacances, le cas échéant)

En utilisant ce modèle, vous pouvez calculer une prévision pour le nombre de clients de chaque jour en copiant la formule suivante de K4 à K5: K257:$ O $ 26 + RECHERCHEV (B4, $ N $ 14: $ O $ 25,2) + RECHERCHEV (D4, $ N $ 4: $ O $ 8,2) + G4 * $ O $ 9 + H4 * $ O $ 10 + I4 * $ O 11 $ + J4 * $ O 12 $

La cellule O26 reprend le terme constant. VLOOKUP (B4, $ N $ 14: $ O $ 25,2) récupère le coefficient du mois pour le mois en cours, et VLOOKUP (D4, $ N $ 4: $ O $ 8,2) récupère le coefficient du jour de la semaine pour le courant la semaine. G4 * $ O 9 $ + H4 * $ O 10 $ + I4 * $ O 11 $ + J4 * $ O 12 $ récupère les effets (le cas échéant) lorsque le jour en cours est codé SP, FAC, BH ou AH.

En copiant la formule (E4-K4) ^ 2 de L4 à L5: L257, vous pouvez calculer l’erreur quadratique pour chaque jour. Ensuite, dans la cellule L2, calculez la somme des erreurs quadratiques avec la formule SOMME (L4: L257).

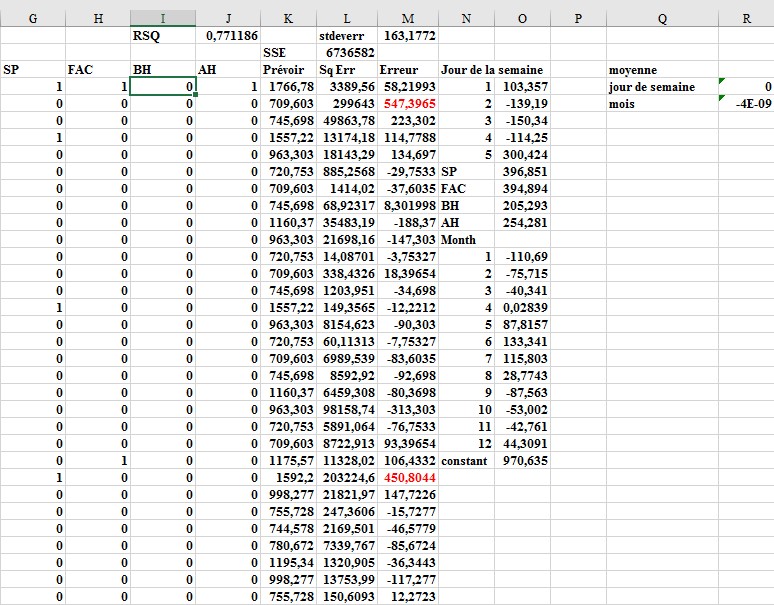
FIGURE 2 Modification des cellules et des prévisions client.

Dans la cellule R4, faites la moyenne des cellules changeant le jour de la semaine avec la formule MOYENNE (O4: O8) et dans la cellule R5, faites la moyenne des cellules changeant le mois avec la formule MOYENNE (O14: O25). Plus tard, vous pouvez limiter les effets moyens du mois et du jour de la semaine à 0, ce qui garantit qu’un mois ou un jour de la semaine avec un effet positif a un nombre de clients supérieur à la moyenne et un mois ou un jour de la semaine avec un effet négatif a un nombre de clients inférieur à la moyenne.

Vous pouvez utiliser le Sol voir les paramètres illustrés à la figure 3 pour choisir les paramètres de prévision afin de minimiser la somme des erreurs quadratiques.

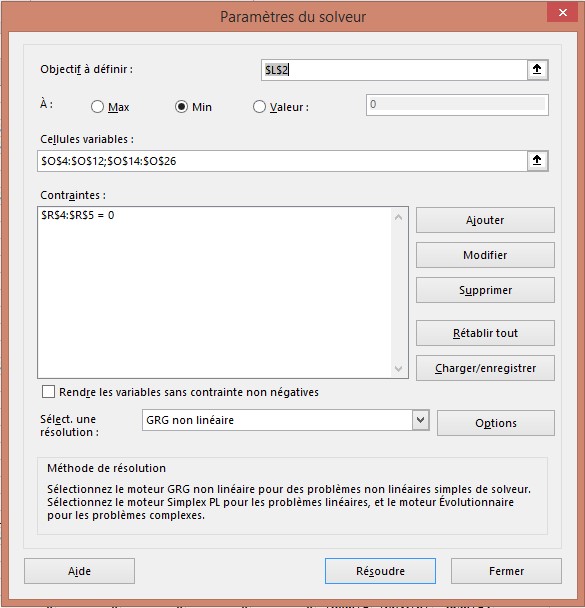
FIGURE 3 Boîte de dialogue Paramètres du solveur pour déterminer les paramètres de prévision.

Le modèle Solver modifie les coefficients pour le mois, le jour de la semaine, BH, AH, SP, FAC et la constante pour minimiser la somme des erreurs carrées. Vous pouvez également contraindre le jour moyen de l’effet semaine et mois à 0. Utilisez le solveur pour obtenir les résultats illustrés à la figure 2. Pour Par exemple, vendredi est le jour le plus chargé de la semaine et juin est le mois le plus chargé. Un salaire du personnel augmente la prévisions (toutes choses égales par ailleurs – en latin, ceteris paribus) par 397 clients.

Comment puis-je évaluer l’exactitude des prévisions?

Pour évaluer la précision de la prévision, vous calculez la valeur R au carré entre les prévisions et le nombre réel de clients dans la cellule J1. La formule que vous utilisez est RSQ (E4: E257, K4: K257). Cette formule calcule le pourcentage de la variation réelle du nombre de clients qui est expliqué par le modèle de prévision. Ici, les variables indépendantes expliquent 77% de la variation quotidienne du nombre de clients.

Vous calculez l’erreur pour chaque jour dans la colonne M en copiant la formule E4 – K4 de M4 à M5: M257. Une approximation proche de l’erreur type de la prévision est donnée par l’écart type des erreurs. Cette valeur est calculée dans la cellule M1 en utilisant la formule STDEVS (M4: M257). Ainsi, environ 68% des prévisions devraient être exactes chez 163 clients, 95% exactes chez 326 clients, etc.

Essayez de repérer les valeurs aberrantes. Rappelons qu’une observation est une valeur aberrante si la valeur absolue d’une erreur de prévision dépasse deux fois l’erreur standard de la régression. Sélectionnez la gamme M4: M257 puis cliquez sur Mise en forme conditionnelle sous l’onglet Accueil. Ensuite, sélectionnez Nouvelle règle et, dans la boîte de dialogue Nouvelle règle de formatage, choisissez Utiliser une formule pour déterminer les cellules à formater. Remplissez la description de la règle dans la boîte de dialogue, comme illustré à la figure 4. (Pour plus d’informations sur le formatage conditionnel, voir l’article 23, «Formatage conditionnel».)

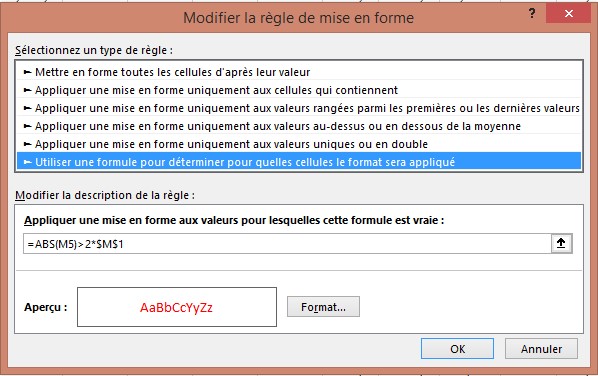
FIGURE 4 Utilisation d’un formatage conditionnel pour repérer les valeurs aberrantes de prévision.

Après avoir choisi un format avec une police rouge, les paramètres de formatage conditionnel s’affichent dans rouge toute erreur supérieure à 2 * (écart type des erreurs) en erreur absolue. En regardant les valeurs aberrantes, vous pouvez voir que le modèle sous-estime souvent le nombre de clients pour les trois premiers jours du mois. De plus, au cours de la deuxième semaine de mars (relâche scolaire), le modèle sur-prévoit et la veille de la relâche scolaire, il sous-estime considérablement.

Pour remédier à ce problème, dans la feuille de calcul 1st Three Days, des cellules changeantes ont été ajoutées pour chacun des trois premiers jours du mois et pour les vacances de printemps et la veille des vacances de printemps. Des valeurs d’essai ont été ajoutées pour ces nouveaux effets dans les cellules O26: O30. En copiant la formule suivante de K4 à K5: K257: $ O $ 25 + RECHERCHEV (B4, $ N $ 13: $ O $ 24,2) + RECHERCHEV (D4, $ N $ 4: $ O $ 8,2) + G4 * $ O $ 9 + H4 * $ O $ 10 + I4 * $ O 11 $ + J4 * $ O 12 $ + SI (C4 = 1, $ O $ 26, SI (C4 = 2, $ O $ 27, SI (C4 = 3, $ O $ 28,0)))

les effets des trois premiers jours du mois sont inclus. (Le terme SI (C4 = 1, O $ 26 $, SI (C4 = 2, O $ 27 $, SI (C4 = 3, O $ 28,0))) reprend l’effet des trois premiers jours du mois. ) Les coefficients de la semaine de relâche ont été saisis manuellement dans les cellules K52: K57. Par exemple, dans la cellule K52, + O29 a été ajouté à la formule et dans les cellules K53: K57, + O30 a été ajouté.

Après avoir inclus les nouvelles cellules changeantes dans la boîte de dialogue Solveur, vous obtenez les résultats affichés dans la figure 5. Notez que les trois premiers jours du mois augmentent considérablement le nombre de clients (probablement parce que du gouvernement et des chèques de sécurité sociale) et que les vacances de printemps réduisent le nombre de clients. La figure 5 montre également l’amélioration de la précision des prévisions. La valeur au carré R (RSQ) s’est améliorée à 87% et l’erreur standard est réduite à 122 clients.

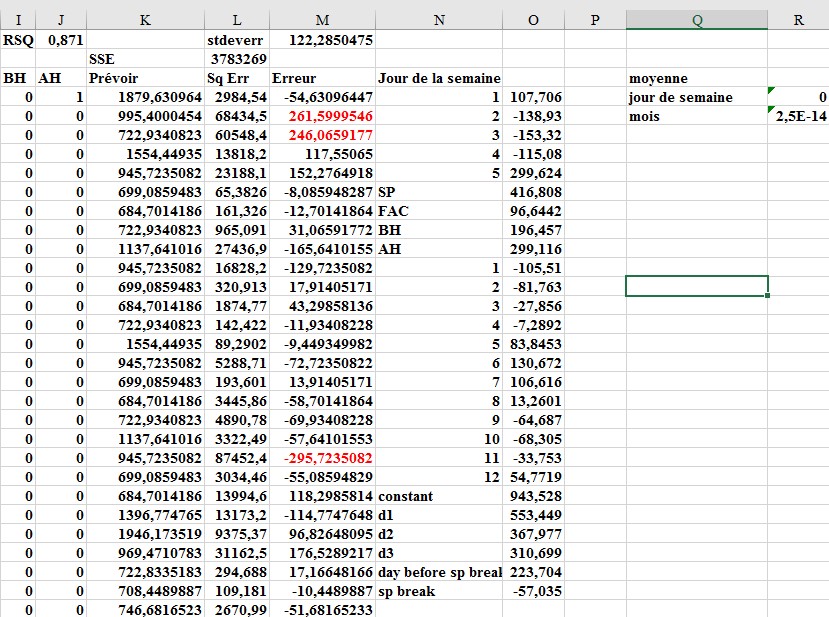
FIGURE 5 Paramètres de prévision et prévisions, y compris les vacances de printemps et les trois premiers jours du mois.

En examinant les erreurs de prévision pour la semaine du 24/12 au 31/12 (voir figure 6), vous pouvez voir que le modèle a considérablement surestimé le nombre de clients pour les jours de cette semaine. Il a également sous-estimé le nombre de clients pour la semaine précédant Noël. Un examen plus approfondi des erreurs de prévision (souvent appelées résidus) montre également ce qui suit:

■■ Thanksgiving est différent des vacances normales en ce sens que la caisse est beaucoup moins occupée que prévu le lendemain de Thanksgiving.

■■ La veille du Vendredi Saint est très chargée car les gens quittent la ville pour Pâques.

■■ La journée fiscale (16 avril) est également plus occupée que prévu.

■■ La semaine précédant le début des cours d’automne à l’Université d’Indiana (la semaine dernière en août) n’a pas été occupée, probablement parce que de nombreux membres du personnel et du corps professoral prennent des vacances d’été avant la frénésie du semestre d’automne.

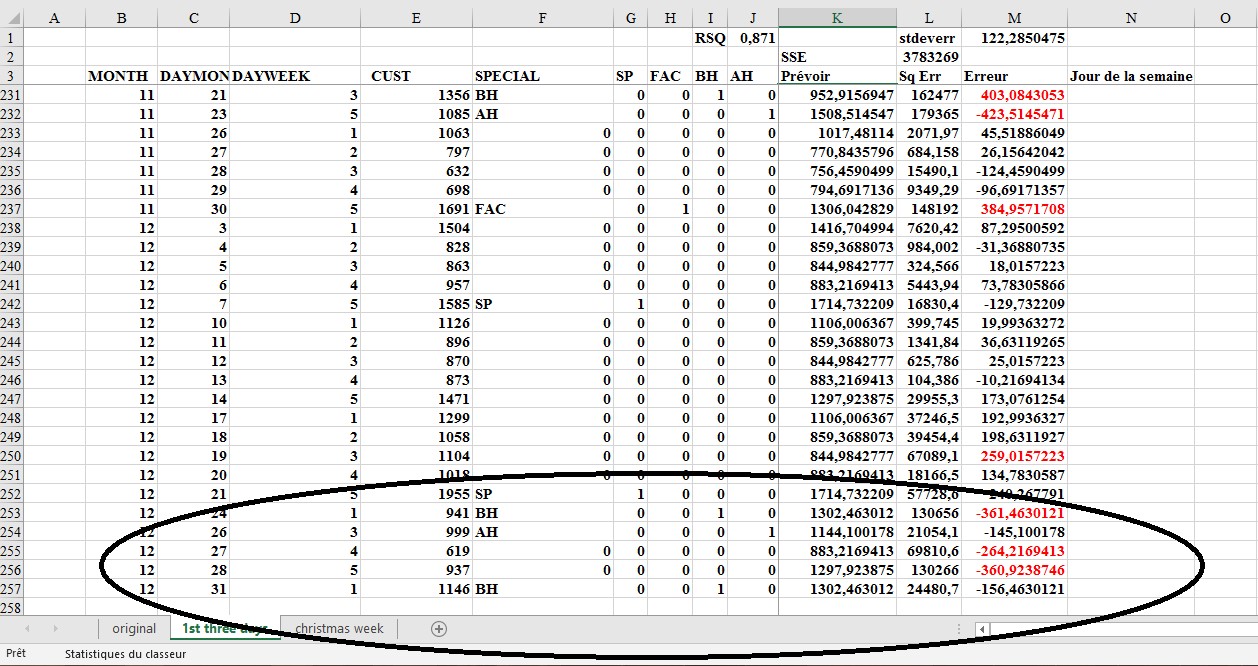
FIGURE 6 Erreurs pour la semaine de Noël.

Dans la feuille de travail de la semaine de Noël, des cellules changeantes ont été ajoutées pour incorporer les effets de ces facteurs. Après avoir ajouté le nouveau paramètre   comme cellules changeantes, exécutez à nouveau Solver. Les résultats que vous devriez obtenir sont présentés dans la figure 65-7. Le RSQ est jusqu’à 92 pour cent, et l’erreur standard est en baisse à 98,61 clients! Notez que l’effet après la semaine de Noël a réduit le nombre de clients quotidiens de 359, la veille de l’Action de grâces ajouté 607 clients, le lendemain de Thanksgiving a réduit le nombre de clients de 161, et ainsi de suite.

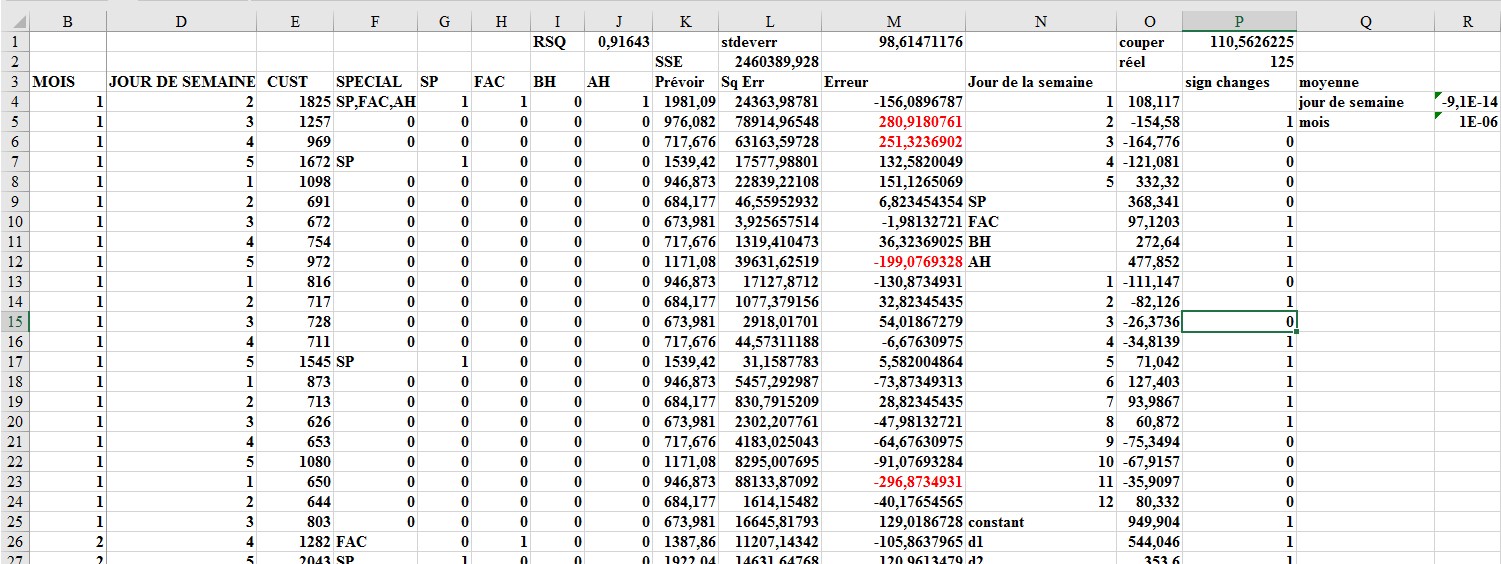
FIGURE 7 Paramètres de prévision finale.

Notez également comment le modèle de prévision est amélioré en utilisant des valeurs aberrantes. Si vos valeurs aberrantes ont quelque chose en commun (comme les trois premiers jours du mois), incluez le facteur commun comme variable indépendante et votre erreur de prévision diminuera.

Comment puis-je vérifier si mes erreurs de prévision sont aléatoires?

Une bonne méthode de prévision devrait créer des erreurs de prévision ou des résidus aléatoires. Par erreurs aléatoires, je veux dire que vos erreurs ne présentent aucun modèle discernable. Si les erreurs de prévision sont aléatoires, le signe de vos erreurs devrait changer (de plus à moins ou de moins à plus) environ la moitié du temps.

Par conséquent, un test couramment utilisé pour évaluer le caractère aléatoire des erreurs de prévision consiste à examiner le nombre de changements de signe dans les erreurs. Si vous avez n observations, le caractère non aléatoire des erreurs est indiqué si vous trouvez soit moins de:

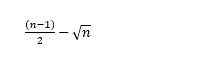
ou plus de:

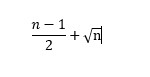
changements de signe. Dans la feuille de travail de la semaine de Noël, comme le montre la figure 7, le nombre de changements de signe a été déterminé dans les résidus en copiant la formule SI(M5 * M4 <0,1,0) de la cellule P5 à P6: P257. Un changement de signe dans les résidus se produit si et seulement si le produit de deux résidus consécutifs est négatif. Par conséquent, cette formule donne 1 chaque fois qu’un changement du signe des résidus se produit. Il y a eu 125 changements de signe. Dans la cellule P1:

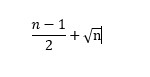
les changements ont été calculés en signe comme seuil pour les résidus non aléatoires. Par conséquent, vous avez des résidus aléatoires.

Une analyse similaire a été effectuée pour prédire le nombre quotidien de clients pour le dîner dans une grande chaîne de restaurants. Les facteurs particuliers correspondaient aux vacances. L’étude a révélé que le Super Sunday (le jour du Super Bowl de la NFL) était la journée la moins occupée et que la Saint-Valentin et la Fête des mères étaient les plus occupées. De plus, le samedi était le jour le plus occupé de la semaine pour le dîner et le vendredi était le jour le plus occupé de la semaine pour le déjeuner.