■ Qui utilise la simulation Monte Carlo?

■ Que se passe-t-il lorsque je tape = ALEA() dans une cellule?

■ Comment puis-je simuler les valeurs d’une variable aléatoire discrète?

■ Comment puis-je simuler les valeurs d’une variable aléatoire normale?

■ Comment une société de cartes de vœux peut-elle déterminer le nombre de cartes à produire?

Qui utilise la simulation Monte Carlo?

De nombreuses entreprises utilisent la simulation Monte Carlo comme une partie importante de leur processus décisionnel. Voici quelques exemples:

■ General Motors, Proctor and Gamble, Pfizer, Bristol-Myers Squibb et Eli Lilly utilisent la simulation pour estimer à la fois le rendement moyen et le facteur de risque des nouveaux produits. Chez GM, l’ancien PDG Rick Waggoner a utilisé ces informations pour déterminer quels produits étaient commercialisés.

■ GM utilise la simulation pour des activités telles que la prévision du revenu net de la société, la prévision des coûts structurels et d’achat et la détermination de sa sensibilité à différents types de risques (tels que les variations des taux d’intérêt et les fluctuations des taux de change).

■ Lilly utilise la simulation pour déterminer la capacité optimale de l’usine pour chaque médicament.

■ Proctor and Gamble utilise la simulation pour modéliser et couvrir de manière optimale le risque de change.

■ Sears utilise la simulation pour déterminer combien d’unités de chaque gamme de produits doivent être commandées auprès des fournisseurs, par exemple, le nombre de paires de pantalons Dockers à commander cette année.

■ Les sociétés pétrolières et pharmaceutiques utilisent la simulation pour évaluer des options réelles telles que la valeur d’une option pour étendre, contracter ou reporter un projet.

■ Les planificateurs financiers utilisent la simulation Monte Carlo pour déterminer les stratégies d’investissement optimales pour la retraite de leurs clients.

Que se passe-t-il lorsque je tape = ALEA () dans une cellule?

Lorsque vous tapez la formule = ALEA () dans une cellule, vous obtenez un nombre qui est également susceptible de prendre n’importe quelle valeur entre 0 et 1. Ainsi, environ 25% du temps, vous devez obtenir un nombre inférieur ou égal à 0,25 ; environ 10% du temps, vous devriez obtenir un nombre d’au moins 0,90, et ainsi de suite. Pour illustrer le fonctionnement de la fonction ALEA, consultez le fichier, illustré à la figure 1.

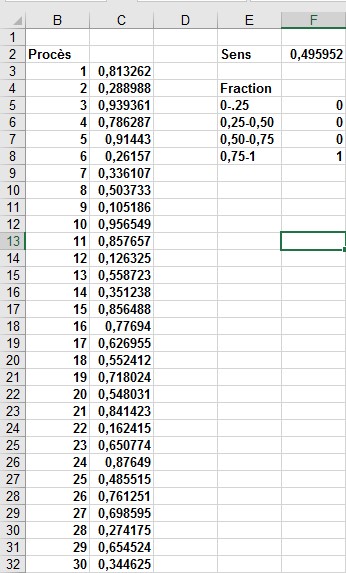
FIGURE 1 Présentation de la fonction ALEA.

Remarquer que lorsque vous ouvrez la feuille de calcul Feuil1, vous ne verrez pas le mêmes nombres aléatoires illustrés à la figure 1. La fonction ALEA recalcule toujours lees nombres générés lors de l’ouverture d’une feuille de calcul ou lors de la saisie de nouvelles informations dans la feuille de calcul. Les valeurs de la feuille de calcul sont fixées pour correspondre à la figure 1.

La formule = ALEA () a été copiée de la cellule C3 vers C4: C402; la plage C3: C402 a été nommée Data. Ensuite, dans la colonne F, vous pouvez suivre la moyenne des 400 nombres aléatoires (cellule F2) et utiliser la fonction NB.SI pour déterminer les fractions comprises entre 0 et 0,25, 0,25 et 0,50, 0,50 et 0,75 et 0,75 et 1. Lorsque vous appuyez sur la touche F9, les nombres aléatoires sont recalculés. Notez que la moyenne des 400 nombres est toujours d’environ 0,5 et qu’environ 25% des résultats sont à des intervalles de 0,25. Ces résultats sont cohérents avec la définition d’un nombre aléatoire. Notez également que les valeurs générées par ALEA dans différentes cellules sont indépendantes. Par exemple, si le nombre aléatoire généré dans la cellule C3 est un grand nombre (par exemple, 0,99), cela ne vous dit rien sur les valeurs des autres nombres aléatoires générés.

Comment puis-je simuler les valeurs d’une variable aléatoire discrète?

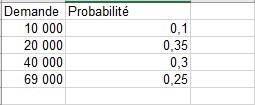
Supposons que la demande d’un calendrier soit régie par la variable aléatoire discrète suivante:

Comment pouvez-vous faire jouer Excel, ou simuler, cette demande de calendriers plusieurs fois? L’astuce consiste à associer chaque valeur possible de la fonction ALEA à une éventuelle demande de calendriers. L’affectation suivante garantit qu’une demande de 10 000 se produira 10% du temps, et ainsi de suite:

Pour illustrer la simulation de la demande, consultez la feuille de calcul Sim dans le fichier (ou sa version congelée illustrée à la figure 2).

FIGURE 2 Simulation d’une variable aléatoire discrète.

La clé de cette simulation consiste à utiliser un nombre aléatoire pour lancer une recherche à partir de la plage de table F2: G5 (appelée recherche). Des nombres aléatoires supérieurs ou égaux à 0 et inférieurs à 0,10 donneront une demande de 10 000; des nombres aléatoires supérieurs ou égaux à 0,10 et inférieurs à 0,45 donneront une demande de 20 000; des nombres aléatoires supérieurs ou égaux à 0,45 et inférieurs à 0,75 seront donner une demande de 40 000; et des nombres aléatoires supérieurs ou égaux à 0,75 donneront une demande de 69 000. Quatre cents nombres aléatoires ont été générés en copiant la formule ALEA () de C3 à C4: C402. Ensuite, 400 essais, ou itérations, de la demande de calendrier ont été générés en copiant le RECHERCHEV (C3, recherche, 2) formule de B3 à B4: B402. Cette formule garantit que tout nombre aléatoire inférieur à 0,10 génère une demande de 10 000; tout nombre aléatoire compris entre 0,10 et 0,45 génère une demande de 20 000; etc. Dans la plage de cellules F8: F11, la fonction NB.SI a été utilisée pour déterminer la fraction des 400 itérations générant chaque demande. Lorsque vous appuyez sur F9 pour recalculer les nombres aléatoires, les probabilités simulées sont proches des probabilités de demande supposées.

Comment puis-je simuler les valeurs d’une variable aléatoire normale? 

Si vous tapez la formule LOI.NORMALE.INVERSE.N (alea (), mu, sigma) dans n’importe quelle cellule, vous générez une valeur simulée d’une variable aléatoire normale ayant un Mu moyen et un écart-type sigma. Cette procédure est illustrée dans la feuille de calcul Sim du fichier Normalsim.xlsx. (Voir la figure 3 pour la version gelée.)

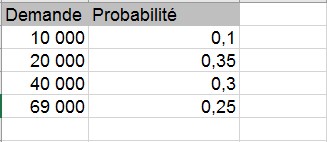
FIGURE 3 Simulation d’une variable aléatoire normale.

Supposons que vous souhaitiez simuler 400 essais pour une variable aléatoire normale avec une moyenne de 40 000 et un écart-type de 10 000. (Ces valeurs sont saisies dans les cellules E1 et E2, et ces cellules sont nommées moyenne et sigma, respectivement.) Copie de la formule = RAND () de C4 à C5: C403 génère 400 nombres aléatoires. Copie de la formule NORM.INV (C4, moyenne, sigma) de B4 à B5: B403 génère 400 valeurs d’essai à partir d’une variable aléatoire normale avec une moyenne de 40 000 et un écart-type de 10 000. Lorsque vous appuyez sur la touche F9 pour recalculer les nombres aléatoires, la moyenne reste proche de 40 000 et l’écart-type près de 10 000.

Essentiellement, pour un nombre aléatoire p, la formule NORM.INV (p, moyenne, sigma) génère le p centième d’une variable aléatoire normale avec une moyenne Mu et un écart-type Sigma. Par exemple, le nombre aléatoire 0,87 dans la cellule C4 (voir la figure 3) génère approximativement le quatre-vingt-septième centile d’une variable aléatoire normale avec une moyenne de 40 000 et un écart-type de 10 000 dans la cellule B4.

Comment une société de cartes de vœux peut-elle déterminer le nombre de cartes à produire?

Cette section montre comment la simulation Monte Carlo peut être utilisée comme outil de prise de décision. Supposons que la demande d’une carte de Saint Valentin soit régie par la variable aléatoire discrète suivante :

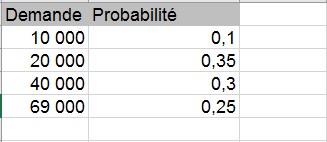
La carte de vœux se vend 4,00 $ et le coût variable de production de chaque carte est de 1,50 $. Les cartes restantes doivent être éliminées au coût de 0,20 $ par carte. Combien de cartes doivent être imprimées?

Fondamentalement, vous simulez plusieurs fois chaque quantité de production possible (10 000; 20 000; 40 000 ou 69 000) (par exemple, mille itérations). Ensuite, vous déterminez quelle quantité de commande génère le profit moyen maximum sur les mille itérations. Vous pouvez trouver les données de cette section dans la feuille de calcul Sim du fichier. (La version gelée est illustrée à la figure 4.) Les noms de plage dans les cellules B1: B11 ont été attribués aux cellules C1: C11. Le nom Recherche a été attribué à la plage de cellules G3: H6. Les paramètres de prix de vente et de coût sont saisis dans les cellules C4: C6.

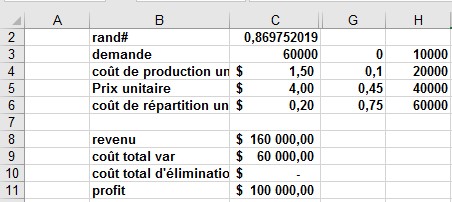
FIGURE 4 Simulation de la carte de la Saint-Valentin.

Entrez une quantité de production d’essai (40 000 dans cet exemple) dans la cellule C1. Créez un nombre aléatoire dans la cellule C2 avec la formule = ALEA (). Comme décrit précédemment, la demande pour la carte dans la cellule C3 est simulée avec la formule RECHERCHEV (rand, recherche, 2). (Dans la formule RECHERCHEV, rand est le nom de cellule affecté à la cellule C3, pas la fonction ALEA.)

Le nombre d’unités vendues est le moindre de la quantité et de la demande de production. Dans la cellule C8, calculez le revenu avec la formule MIN (produit, demande) * prix unitaire. Dans la cellule C9, calculez le coût de production total avec la formule * unit_prod_cost produite.

Si plus de cartes sont produites que ce qui est demandé, le nombre d’unités restantes est égal à la production moins la demande; sinon, aucune unité n’est laissée. Calculez le coût d’élimination dans la cellule C10 avec la formule unit_ disp_cost * SI (produit> demande, produit – demande, 0). Enfin, dans la cellule C11, calculez le bénéfice en tant que revenu – total_var_cost-total_disposing_cost.

Ce serait bien d’avoir un effectif   moyen efficace d’appuyer plusieurs fois sur F9 (par exemple, mille) pour chaque quantité de production et de calculer le bénéfice escompté pour chaque quantité. Cette situation est celle dans laquelle un tableau de données bidirectionnel vient à la rescousse. (Voir l’article 16, «Analyse de sensibilité avec des tableaux de données», pour plus de détails sur les tableaux de données.) Le tableau de données utilisé dans cet exemple est illustré à la figure 5.

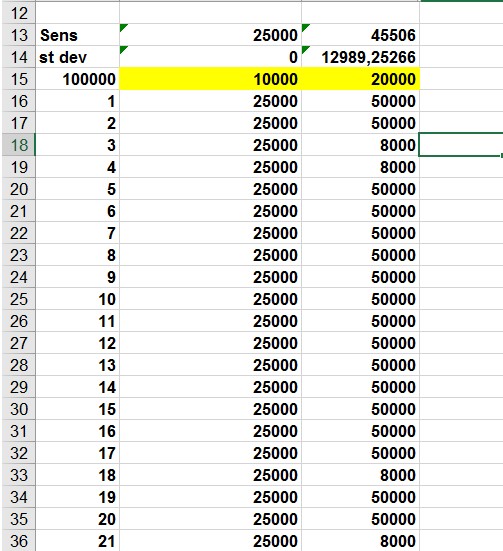
FIGURE 5 Tableau de données bidirectionnel pour la simulation de carte de voeux.

Dans la plage de cellules A16: A1015, entrez les nombres 1 à 1 000 (correspondant aux 1 000 essais). Une façon simple de créer ces valeurs consiste à commencer par entrer 1 dans la cellule A16. Sélectionnez la cellule, puis, dans l’onglet Accueil du groupe Édition, cliquez sur Remplir (l’icône avec la flèche vers le bas), puis sélectionnez Série pour ouvrir la boîte de dialogue Série. Dans la boîte de dialogue Série, illustrée à la figure 73-6, entrez une valeur de pas de 1 et une valeur d’arrêt de 1 000. Dans la zone Series In, sélectionnez Columns puis cliquez sur OK. Les chiffres de 1 à 1000 seront inscrits dans la colonne A, en commençant dans la cellule A16.

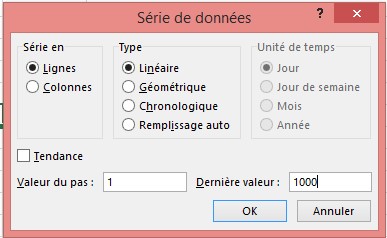
FIGURE 6 Utilisation de la boîte de dialogue Série pour remplir les numéros d’essai 1 à 1 000.

Saisissez les quantités de production possibles (10 000; 20 000; 40 000; 69 000) dans les cellules B15: E15. Vous souhaitez calculer le bénéfice pour chaque numéro d’essai (1 à 1 000) et chaque quantité de production. Reportez-vous à la formule de profit (calculée dans la cellule C11) dans la cellule supérieure gauche du tableau de données (A15) en entrant = C11.

Vous pouvez désormais inciter Excel à simuler mille itérations de demande pour chaque quantité de production. Sélectionnez la plage de tableaux (A15: E1015), puis, dans le groupe Outils de données de l’onglet Données, cliquez sur Utilisataire d’analyse, puis sélectionnez Tableau de données. Pour configurer un tableau de données bidirectionnel, choisissez la quantité de production (cellule C1) comme cellule d’entrée de ligne et sélectionnez n’importe quelle cellule vide (la cellule I14 a été choisie ici) comme cellule d’entrée de colonne. Après avoir cliqué sur OK, Excel simule mille valeurs de demande pour chaque quantité de commande.

Pour comprendre pourquoi cela fonctionne, tenez compte des valeurs placées par le tableau de données dans la plage de cellules C16: C1015. Pour chacune de ces cellules, Excel utilise une valeur de 20 000 dans la cellule C1. En C16, la valeur de cellule d’entrée de colonne de 1 est placée dans une cellule vide et le nombre aléatoire dans la cellule C2 recalcule. Le bénéfice correspondant est ensuite enregistré dans la cellule C16. Ensuite, la valeur de cellule d’entrée de colonne de 2 est placée dans une cellule vide, et le nombre aléatoire dans C2 recalcule à nouveau. Le bénéfice correspondant est inscrit dans la cellule C17.

En copiant la formule MOYENNE (B16: B1015) de la cellule B13 vers C13: E13, vous pouvez calculer la moyenne bénéfice simulé pour chaque quantité de production. En copiant la formule STDEV (B16: B1015) de la cellule B14 à C14: E14, vous pouvez calculer l’écart type des bénéfices simulés pour chaque quantité d’ordre. Chaque fois que vous appuyez sur F9, mille itérations de demande sont simulées pour chaque quantité de commande. La production de 40 000 cartes produit toujours le plus grand bénéfice attendu, donc la production de 40 000 cartes semble être la bonne décision.

l’impact du risque sur votre décision Si vous produisez 20 000 cartes au lieu de 40 000, le bénéfice escompté baisse d’environ 22%, mais le risque (mesuré par l’écart type du profit) chute de près de 73%. Par conséquent, si vous êtes extrêmement opposé au risque, produire 20 000 cartes pourrait être la bonne décision. Soit dit en passant, la production de 10 000 cartes a toujours un écart-type de 0 carte, car si vous produisez 10 000 cartes, vous les vendrez toutes sans restes.

        Remarque Dans ce classeur, j’ai défini l’option de calcul sur Automatique sauf pour les tables. (Utilisez la commande Calcul dans le groupe Calcul de l’onglet Formules.) Ce paramètre permet

s’assure que le tableau de données ne recalcule pas sauf si vous appuyez sur F9, ce qui est une bonne idée car un grand tableau de données ralentira votre travail s’il recalcule chaque fois que vous tapez quelque chose dans votre feuille de calcul. Notez que dans cet exemple, chaque fois que vous appuyez sur F9, le profit moyen change. Cela se produit car chaque fois que vous appuyez sur F9, une séquence différente de mille nombres aléatoires est utilisée pour générer des demandes pour chaque quantité de commande.

Intervalle de confiance pour le profit moyen

Une question naturelle à poser dans cette situation est: «Dans quel intervalle serai-je sûr à 95% que le vrai signifie que le profit va baisser? ” Cet intervalle est appelé intervalle de confiance à 95% pour le profit moyen. Un intervalle de confiance de 95% pour la moyenne de toute sortie de simulation est calculé par la formule suivante:

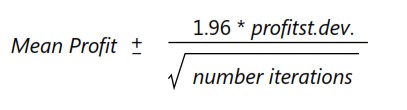
Dans la cellule J11, vous pouvez calculer la limite inférieure de l’intervalle de confiance à 95% sur le bénéfice moyen lorsque 40 000 calendriers sont produits avec la formule D13–1,96 * D14 / SQRT (1000). Dans la cellule J12, la limite supérieure de l’intervalle de confiance à 95% a été calculée avec la formule D13 + 1,96 * D14 / SQRT (1000). Ces calculs sont illustrés à la figure 7.

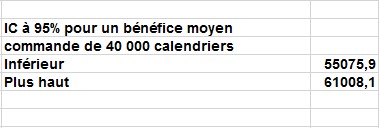
FIGURE 7 Intervalle de confiance à 95% pour le bénéfice moyen lorsque 40 000 calendriers sont commandés.

Vous pouvez être sûr à 95% que votre bénéfice moyen lorsque 40000 calendriers sont commandés est entre     en 55 076 $ et 61 008 $.