Je discute de l’écart-type et des scores z, et montre comment vous pouvez exprimer une valeur en unités d’écart-type. Par exemple, si vous avez un échantillon de 10 personnes dont la taille moyenne est de 68 pouces avec un écart-type de

4 pouces, vous pouvez exprimer une taille de 72 pouces comme un écart-type au-dessus de la moyenne ou, de manière équivalente, score de +1.0. Ce faisant, cela supprime les attributs de l’échelle de mesure originale et rend les comparaisons entre différentes variables beaucoup plus claires.
Le score z est calculé, et donc standardisé, en soustrayant la moyenne d’une valeur donnée et en divisant le résultat par l’écart-type. Le coefficient de corrélation utilise un calcul analogue. Pour revoir, la formule de définition du coefficient de corrélation est
r = Sxy / SxSy
ou, en mots, la corrélation est égale à la covariance divisée par le produit des écarts-types des deux variables. Il est donc normalisé de 0 à plus ou moins 1,0, sans être influencé par les unités de mesure utilisées dans les variables sous-jacentes.
La covariance, comme la variance, peut être difficile à visualiser. Supposons que vous ayez les poids en livres des mêmes 10 personnes, ainsi que leurs tailles. Vous pouvez calculer la moyenne de leurs poids à 150 livres et l’écart-type de leurs poids à 25 livres. Il est facile de voir une distance de 25 livres sur l’axe horizontal d’une carte. Il est plus difficile de visualiser la variance de votre échantillon, qui est de 625 livres au carré, ou même de comprendre sa signification.

De même, il peut être difficile de comprendre la signification de la covariance (à moins que vous ayez l’habitude de travailler avec les mesures concernées, ce qui est souvent le cas pour les physiciens et les ingénieurs), ils connaissent généralement la covariance des mesures avec lesquelles ils travaillent et parfois terme le coefficient de corrélation la covariance sans dimension).
Dans votre échantillon de 10 personnes, par exemple, vous pourriez avoir des mesures de taille ainsi que des mesures de poids. Si vous calculez la covariance de la taille et du poids dans votre échantillon, vous pourriez vous retrouver avec une valeur telle que 58,5 pieds-livres. Mais ce n’est pas une des significations classiques de «pied-livre», une mesure de force ou d’énergie. C’est une mesure de la façon dont les livres et les pieds se combinent dans votre échantillon. Et la façon dont vous visualisez ou interprétez cette mesure n’est pas toujours claire.
Le coefficient de corrélation résout cette difficulté d’une manière similaire au z-score. Vous divisez la covariance par l’écart-type de chaque variable, supprimant ainsi l’effet des deux échelles – ici, la taille et le poids – et il vous reste une expression de la force de la relation qui n’est pas affectée par votre choix de mesurer, que ce soit des pieds ou des pouces ou des centimètres, ou des livres ou des onces ou des kilogrammes. Une relation parfaite, un-à-un est plus ou moins 1.0. L’absence de relation est de 0.0. Les corrélations de la plupart des variables se situent quelque part entre les extrêmes.

Dans le z-score, vous avez un moyen de mesurer à quelle distance de la moyenne une personne ou un objet est trouvé, sans référence à l’unité de mesure. Peut-être la taille de John est de 70,8 pouces, ou un z-score sur la hauteur de 0,70. Peut-être que la corrélation entre la taille et le poids dans votre échantillon – encore une fois, non contaminée par les échelles de mesure – est de 0,65. Vous pouvez maintenant prédire le poids de John avec cette équation:
z_Taille = rz_Poids
La distance prédite par John de la moyenne sur le poids est le produit du coefficient de corrélation et de sa distance à la moyenne sur la taille. Plus précisément, le z-score prédictif de John sur le poids est égal à la corrélation r fois son z-score sur la hauteur, ou 0.65 * 0.70 ou 0.455. Voir la figure 4.14 pour les détails.
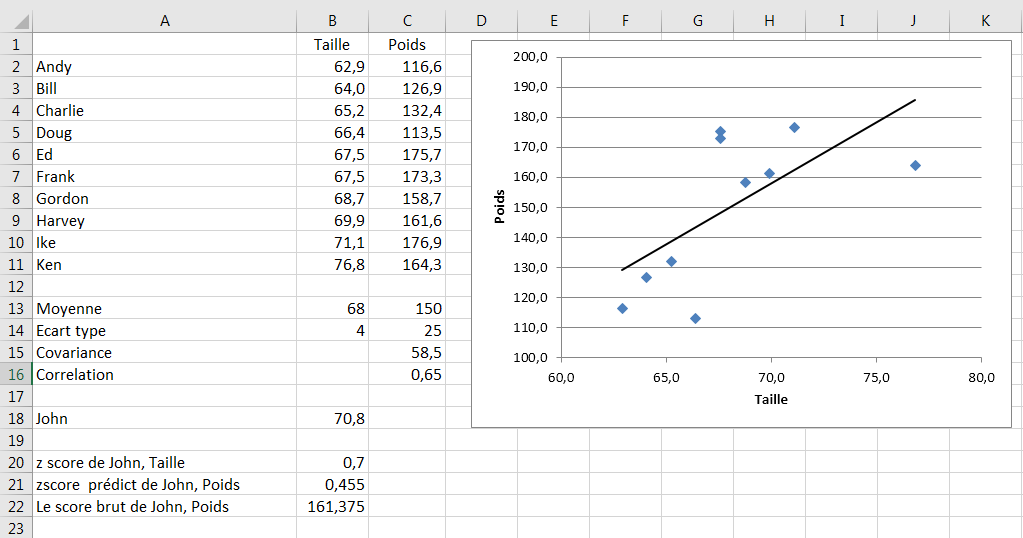
Figure 4.14. La ligne de régression montre où les points de données tomberaient si la corrélation était parfaite.

 
Remarque

Le z-score prédictif que le poids de John (0.455) est plus petit que son z-score sur la taille (0.70). Son poids est censé régresser vers la moyenne sur le poids, tout comme la taille prédite d’un fils est plus proche de la taille moyenne des fils que celle de son père à la hauteur moyenne des pères. Cette régression a toujours lieu lorsque la corrélation n’est pas parfaite: c’est-à-dire quand elle est inférieure à 1,0 et supérieure à -1,0. C’est inhérent à l’équation donnée ci-dessus pour le poids et la taille, répétée ici sous une forme plus générale: z_y = r_xy z_x. Considérez cette équation et gardez à l’esprit que r est toujours compris entre -1,0 et +1,0.
Le poids moyen dans votre échantillon est de 150 livres, et l’écart type est de 25. Vous avez le z-score prédictif de John pour le poids, 0,455, le résultat de multiplier la corrélation par le z-score réel de John pour le poids. Vous pouvez changer ce z-score prédit en livres en réarrangeant la formule pour un z-score:
Z = (X ~ X) / s
X = sz + X
Dans le cas de John, vous avez ce qui suit:
161.375 = 25 * 0.455 + 150
Pour vérifier ce résultat, reportez-vous à la cellule B22 de la Figure 4.14.
Donc, la corrélation de .65 vous conduit à prédire que John pèse 161,375 livres. Mais alors John vous dit qu’il pèse en réalité 155 livres. Lorsque vous utilisez même une corrélation raisonnablement forte pour faire des prédictions, vous ne vous attendez pas à ce que vos prédictions soient exactes fréquence, pas plus que vous ne pensez que la prédiction pour un dixième de pouce de pluie demain soit exactement correcte. Dans les deux cas, cependant, vous vous attendez à ce que la prédiction soit raisonnablement proche la plupart du temps.