Tracer des variables numériques dans Excel
Plusieurs types de graphiques dans Excel se prêtent magnifiquement à la représentation visuelle des variables numériques. Ce cours s’appuie fortement sur des graphiques de ce type parce que la plupart d’entre nous trouvent des
concepts statistiques difficiles à saisir dans l’abstrait qui sont beaucoup plus clairs lorsqu’ils sont illustrés dans des graphiques.
Tracer deux variables
Plus haut dans ce chapitre, je discute brièvement de deux types de graphiques qui utilisent une variable de catégorie sur un axe et une variable numérique sur l’autre: Diagrammes à colonnes et Diagrammes à barres. Il existe d’autres types de graphiques similaires, tels que les graphiques en courbes, qui sont utiles pour analyser une variable numérique en termes de catégories différentes, en particulier les catégories de temps, telles que les mois, les trimestres et les années.
Cependant, un type particulier de graphique Excel, appelé graphique XY (Scatter), montre la relation entre exactement deux variables numériques. La figure 1.8 fournit un exemple.
Figure 1.8. Dans un diagramme XY (Scatter), les axes horizontal et vertical sont des axes de valeur.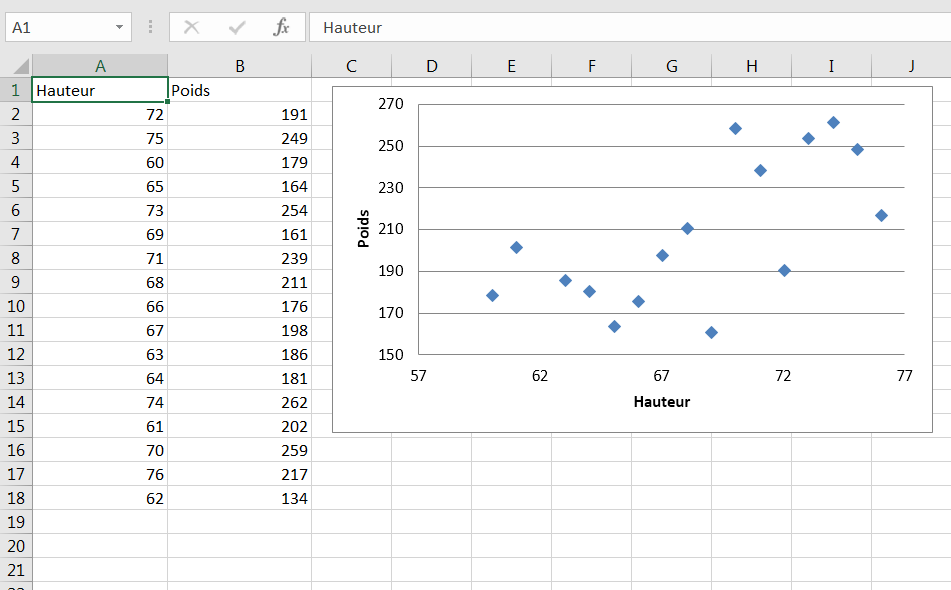
Remarque
Depuis les années 1990 au moins, Excel a appelé ce type de graphique un graphique XY (Dispersion). Dans sa version de 2007, Excel a commencé à se référer à un graphique XY dans certains endroits, à un graphique Dispersion dans d’autres, et à un graphique XY (Dispersion) dans d’autres encore. Pour la plupart, ce cours opte pour la brièveté du graphique XY, et quand vous voyez ce terme, vous pouvez être sûr qu’il est le même qu’un diagramme XY (Dispersion).
Les marqueurs dans un diagramme XY montrent où une personne ou un objet particulier tombe sur chacune des deux variables numériques. Le modèle global des marqueurs peut vous en dire un peu plus sur la relation entre les variables, telle qu’elle est exprimée dans la mesure de chaque enregistrement. Le chapitre 4, «Comment les variables se déplacent conjointement: la corrélation», donne des détails considérables sur ce type de relation.
Dans la figure 1.8, par exemple, vous pouvez voir la relation entre la taille et le poids d’une personne: En général, plus la taille est grande, plus le poids est important. La relation entre les deux variables diffère fondamentalement de celles discutées plus haut dans ce chapitre, où l’accent est mis sur la somme ou la moyenne d’une variable numérique, comme le nombre de véhicules, selon la catégorie d’une variable nominale, telle que voiture.
Cependant, lorsque vous êtes intéressé par la façon dont deux variables numériques sont liées, vous posez une question différente et vous utilisez une analyse statistique différente. Quelle est la relation entre la taille et le poids, et quelle est la force de la relation? Le temps passé sur un téléphone cellulaire correspond-il d’une certaine façon à la probabilité de contracter un cancer? Les gens qui passe plus d’années à l’école finalement faire plus d’argent? (Et si tel est le cas, est-ce que cette relation va de l’école primaire aux études supérieures?) C’est une autre catégorie importante de recherche empirique et d’analyse statistique: l’étude de la façon dont différentes variables changent ensemble. ils covarient.
Les diagrammes XY d’Excel peuvent vous en dire beaucoup sur la façon dont deux variables numériques sont liées. La figure 1.9 ajoute ce qu’Excel appelle une courbe de tendance au graphique XY de la figure 1.8.
Figure 1.9. Une ligne de tendance représente une relation numérique, ce qui n’est presque jamais une façon précise de représenter la réalité.
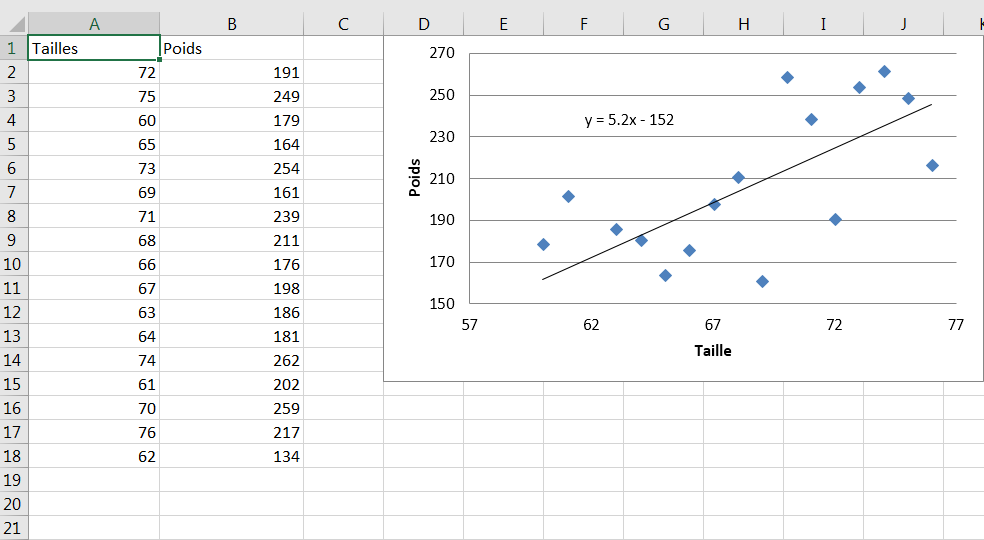
La ligne diagonale que vous voyez dans la figure 1.9 est une ligne de tendance (plus souvent appelée une ligne de régression). C’est une représentation idéalisée de la relation entre la taille et le poids des hommes, au moins telle qu’elle est déterminée à partir de l’échantillon de 17 hommes dont les mesures sont représentées sur la figure. La courbe de tendance est basée sur cette formule:
Poids = 5,2 * Taille – 152
Excel calcule la formule en fonction de ce qu’on appelle le critère des moindres carrés. Vous verrez beaucoup plus à ce sujet dans le chapitre 4.
Supposons que vous ayez choisi plusieurs valeurs de taille, par exemple, 20, les avez branché sur cette formule, puis utilisé la formule pour calculer le poids résultant. Si vous avez maintenant créé un graphique Excel XY qui affiche ces valeurs de tailles et de poids, vous obtenez un graphique qui montre une ligne droite similaire à la ligne de tendance que vous voyez dans la Figure 1.9.
C’est parce que l’arithmétique est agréable et propre et n’implique pas d’erreurs. La formule applique l’arithmétique qui résulte en un ensemble de poids prédits qui, tracés en fonction de la hauteur sur un graphique, décrivent une ligne droite. La réalité, cependant, est rarement exempte d’erreurs. Certaines personnes pèsent plus qu’une formule ne le devrait, compte tenu de leur taille. D’autres personnes pèsent moins. (L’analyse statistique définit ces écarts ou écarts ou résidus.) Le résultat est que si vous tracez les mesures que vous obtenez des personnes réelles plutôt que d’une formule mécanique, vous obtiendrez un ensemble de données qui semblent un peu dispersées. marqueurs dans les figures 1.8 et 1.9.
La réalité est désordonnée, et l’approche du statisticien pour le nettoyer est de chercher à identifier les modèles réguliers qui se cachent derrière les mesures du monde réel. Si ces mesures du monde réel ne correspondent pas exactement au modèle qui a été identifié, il y a plusieurs explications, y compris celles-ci (et elles ne s’excluent pas mutuellement):
• Les gens et les choses ne sont pas toujours conformes aux modèles mathématiques idéaux. Faites avec.
• Il peut y avoir un problème avec la façon dont les mesures ont été prises. Obtenez de meilleurs critères.
• Une autre variable non examinée peut provoquer des écarts par rapport au modèle sous-jacent. Venez avec un peu plus de théorie et ensuite effectuer plus de recherches.
