Une introduction aux variables aléatoires dans Microsoft Excel
■■ Qu’est-ce qu’une variable aléatoire?
■■ Qu’est-ce qu’une variable aléatoire discrète?
■■ Quelle est la moyenne, la variance et l’écart-type d’une variable aléatoire?
■■ Qu’est-ce qu’une variable aléatoire continue?
■■ Qu’est-ce qu’une fonction de densité de probabilité?
■■ Que sont les variables aléatoires indépendantes?
| Dans le monde d’aujourd’hui, la seule chose qui est sûre, c’est que nous sommes confrontés à une grande incertitude. Dans les neuf chapitres suivants, vous trouverez quelques techniques puissantes que vous pouvez utiliser pour incorporer l’incertitude dans les modèles d’entreprise. La pierre angulaire de la modélisation de l’incertitude est de comprendre comment utiliser des variables aléatoires. | |
Qu’est-ce qu’une variable aléatoire?
Toute situation dont l’issue est incertaine est appelée une expérience. La valeur d’une variable aléatoire est basée sur le résultat (incertain) d’une expérience. Par exemple, lancer une paire de dés est une expérience, et une variable aléatoire peut être définie comme la somme des valeurs indiquées sur chaque dé. Dans ce cas, la variable aléatoire pourrait prendre n’importe quelle valeur de 2, 3, etc. jusqu’à 12. Comme autre exemple, considérons l’expérience de vente d’une nouvelle console de jeu vidéo, pour laquelle une variable aléatoire pourrait être définie comme part de marché de ce nouveau produit.
Qu’est-ce qu’une variable aléatoire discrète?
Une variable aléatoire est discrète si elle peut prendre un nombre fini de valeurs possibles. Voilà quelque exemples de variables aléatoires discrètes:
■■ Nombre de concurrents potentiels pour votre produit
■■ Nombre d’As tirés dans une main de poker à cinq cartes
■■ Nombre d’accidents de voiture que vous avez (espérons zéro!) En un an
■■ Nombre de points affichés sur un dé
■■ Nombre de lancers francs sur 12 effectués par la star de Phoenix Sun, Steve Nash, lors d’un match de basket
Quelle est la moyenne, la variance et l’écart-type d’une variable aléatoire?
Dans l’article 42, «Récapitulation des données à l’aide de statistiques descriptives», la moyenne, la variance et l’écart-type d’un ensemble de données ont été examinés. En substance, la moyenne d’une variable aléatoire (souvent désignée par µ) est la valeur moyenne de la variable aléatoire à laquelle vous vous attendez si vous effectuez plusieurs fois une expérience. La moyenne d’une variable aléatoire est souvent appelée la valeur attendue de la variable aléatoire. La variance d’une variable aléatoire (souvent désignée par σ2) est la valeur moyenne de l’écart quadratique par rapport à la moyenne d’une variable aléatoire à laquelle vous vous attendriez si vous effectuiez plusieurs fois une expérience. L’écart type d’une variable aléatoire (souvent notée σ) est simplement la racine carrée de sa variance. Comme pour les ensembles de données, la moyenne d’une variable aléatoire est une mesure récapitulative d’une valeur typique de la variable aléatoire, tandis que la variance et l’écart-type mesurent la propagation de la variable aléatoire autour de sa moyenne.
À titre d’exemple sur la façon de calculer la moyenne, la variance et l’écart-type d’une variable aléatoire, supposons que vous pensez que le rendement du marché boursier au cours de l’année suivante est régi par les probabilités suivantes:
Les calculs manuels montrent ce qui suit:
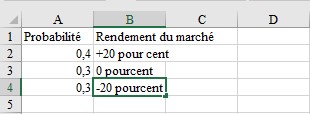
µ = 0,40 * (0,20) + .30 * (0,00) + .30 * (- .20) = 0,02 ou 2 pourcent
σ2 = 0,4 * (0,20 -0,02) 2 + .30 * (0,0 – .02) 2 + .30 * (-0,20 -0,02) 2 = 0,0276
Alors σ = 0,166 ou 16,6%.
Dans le fichier Meanvariance.xlsx (illustré à la figure 1), ces calculs sont vérifiés.
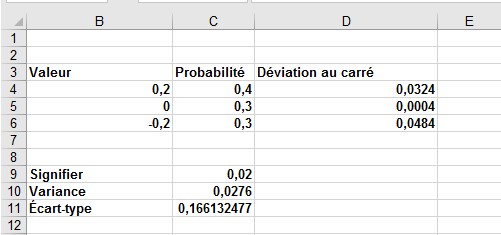
FIGURE 1 Calcul de la moyenne, de l’écart-type et de la variance d’une variable aléatoire.
La moyenne du rendement du marché a été calculée dans la cellule C9 avec la formule SUMPRODUCT (B4: B6, C4: C6). Cette formule multiplie chaque valeur de la variable aléatoire par sa probabilité et résume les produits.
Pour calculer la variance du rendement du marché, l’écart quadratique de chaque valeur de la variable aléatoire a été déterminé à partir de sa moyenne en copiant la formule (B4– $ C $ 9) ^ 2 de D4 à D5: D6. Ensuite, dans la cellule C10, la variance du rendement du marché a été calculée comme l’écart quadratique moyen par rapport à la moyenne avec la formule SUMPRODUCT (C4: C6, D4: D6). Enfin, l’écart type du rendement du marché a été calculé dans la cellule C11 avec la formule SQRT (C10).
Qu’est-ce qu’une variable aléatoire continue?
Une variable aléatoire continue est une variable aléatoire qui peut prendre un très grand nombre ou, à toutes fins utiles, un nombre infini de valeurs. Voici quelques exemples de variables aléatoires continues:
■■ Prix des actions Microsoft dans un an
■■ Part de marché pour un nouveau produit
■■ Taille du marché pour un nouveau produit
■■ Coût de développement d’un nouveau produit
■■ Poids du nouveau-né
■■ QI de la personne
■■ Pourcentage de tir de Dirk Nowitzki à trois points au cours de la saison prochaine
Qu’est-ce qu’une fonction de densité de probabilité?
Une variable aléatoire discrète peut être spécifiée par une liste de valeurs et la probabilité d’occurrence pour chaque valeur de la variable aléatoire. Parce qu’une variable aléatoire continue peut prendre un nombre infini de valeurs, vous ne pouvez pas répertorier la probabilité d’occurrence pour chaque valeur d’une variable aléatoire continue. Une variable aléatoire continue est complètement décrite par sa fonction de densité de probabilité. Par exemple, la fonction de densité de probabilité pour le QI d’une personne choisie au hasard est illustrée à la figure 2.
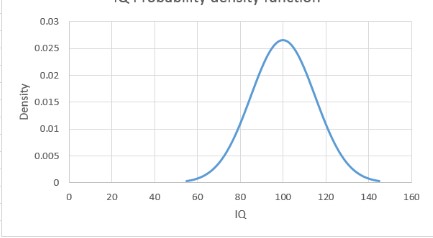
FIGURE 2 Fonction de densité de probabilité pour les QI.
Une fonction de densité de probabilité (pdf) a les propriétés suivantes:
■■ La valeur du pdf est toujours supérieure ou égale à 0.
■■ La zone sous le pdf est égale à 1.
■■ La hauteur de la fonction de densité pour une valeur x d’une variable aléatoire est proportionnelle à la probabilité que la variable aléatoire prenne une valeur proche de x. Par exemple, la hauteur de la densité pour un QI de 83 est à peu près la moitié de la hauteur de la densité pour un QI de 100. Cela vous indique que les QI proches de 83 sont environ deux fois moins probables que les QI autour de 100. En outre, parce que les pics de densité à 100, les QI autour de 100 sont les plus probables.
■■ La probabilité qu’une variable aléatoire continue assume une plage de valeurs est égale à l’aire correspondante sous la fonction de densité. Par exemple, la fraction des personnes ayant des QI de 80 à 100 est simplement la zone sous la densité de 80 à 100.
■■ Notez qu’une variable aléatoire discrète qui suppose de nombreuses valeurs est souvent modélisée comme une variable aléatoire continue. (Voir le chapitre 69, «La variable aléatoire normale».) Par exemple, bien que le nombre de demi-gallons de lait vendus en une seule journée par une petite épicerie soit discret, il s’avère plus pratique de modéliser cette variable aléatoire discrète comme une variable aléatoire continue.
Quelles sont les variables aléatoires indépendantes?
Un ensemble de variables aléatoires est indépendant si la connaissance de la valeur de l’un de ses sous-ensembles ne vous dit rien sur les valeurs des autres variables aléatoires. Par exemple, le nombre de matchs remportés par l’équipe de football de l’Université d’Indiana au cours d’une année est indépendant du pourcentage de retour sur Microsoft au cours de la même année. Le fait de savoir que l’Indiana a très bien réussi ne changerait pas votre vision de la performance de Microsoft au cours de l’année.
Cependant, les rendements des actions Microsoft et Intel ne sont pas indépendants. Si l’on vous dit que les actions de Microsoft ont enregistré un rendement élevé en un an, les ventes d’ordinateurs ont probablement été élevées, ce qui vous indique qu’Intel a probablement également connu une bonne année.
