Il est utile d’utiliser les distributions de fréquence dans l’analyse statistique pour deux raisons générales. L’une concerne la visualisation de la distribution d’une variable entre des personnes ou des objets. L’autre concerne comment faire

des inférences sur une population de personnes ou d’objets sur la base d’un échantillon.

Ces deux raisons aident à définir les deux branches générales de la statistique: les statistiques descriptives et les statistiques inférentielles. Avec les statistiques descriptives telles que les moyennes, les fourchettes de valeurs et les pourcentages ou les nombres, le graphique d’une distribution de fréquence vous permet de mieux comprendre un ensemble de personnes ou de choses, car il vous permet de visualiser le comportement d’une variable.
Dans le domaine des statistiques inférentielles, les distributions de fréquences basées sur des échantillons vous aident à déterminer le type d’analyse que vous devez utiliser pour faire des inférences sur la population. Comme vous le verrez dans les chapitres suivants, les distributions de fréquence vous aident également à visualiser les résultats de certains choix que vous devez faire, tels que la probabilité d’arriver à une mauvaise conclusion.

Visualisation de la distribution: statistiques descriptives
Il est généralement beaucoup plus facile de comprendre une variable – comment elle se comporte dans différents groupes, comment elle peut changer au fil du temps, et même à quoi elle ressemble – quand on la voit dans un graphique. Par exemple, voici la formule de la distribution normale

Et la figure 1.14 montre la distribution normale sous forme de graphique.
Figure 1.14. La courbe normale familière est juste une distribution de fréquence.

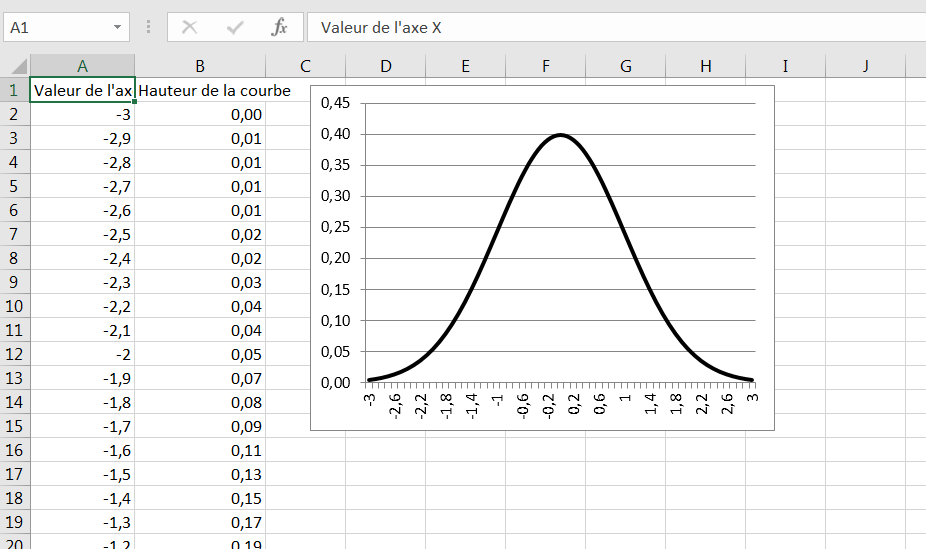
La formule elle-même est indispensable, mais elle ne permet pas de comprendre. En revanche, le graphique vous informe que la distribution de fréquence de la courbe normale est symétrique et que la plupart des enregistrements se regroupent autour du centre de l’axe horizontal.

Remarque
La formule a été développée par un mathématicien français du 17ème siècle nommé Abraham De Moivre. Excel le simplifie à ceci:
= NORMDIST (1,0,1, FALSE)
Depuis Excel 2010, cependant, ça a été le cas:
= NORM.S.DIST (1, FALSE) Ce sont des simplifications majeures.
Encore une fois, la longévité personnelle a tendance à gonfler dans les niveaux les plus élevés de son aire de répartition (et donc à gauche comme dans la figure 1.13). Les prix des maisons ont tendance à augmenter dans les niveaux les plus bas de leur fourchette (et donc faussés). La taille des êtres humains crée un renflement dans le centre de la gamme, et est donc symétrique et non asymétrique.

Certaines analyses statistiques supposent que les données proviennent d’une distribution normale et, dans certaines analyses statistiques, cette hypothèse est importante. Ce cours n’explore pas le sujet en détail parce qu’il se présente rarement. Sachez cependant que si vous voulez analyser une distribution asymétrique, il existe des moyens de la normaliser et donc de se conformer aux hypothèses émises par l’analyse. Très généralement, vous pouvez utiliser les fonctions SQRT () et LOG () d’Excel pour normaliser une distribution biaisée négativement et un opérateur d’exponentiation (par exemple, = A2 ^ 2 pour mettre la valeur en A2) pour normaliser une distribution asymétrique positive.

Remarque
Cependant, trouver la bonne transformation pour un ensemble de données particulier peut être une question d’essai et d’erreur, et le complément Excel Solver peut aider en conjonction avec la fonction SKEW () d’Excel. Pour plus d’informations sur Solver, reportez-vous au chapitre 2, “Comment regrouper les valeurs de cluster”, et au chapitre 7, “Utilisation d’Excel avec la distribution normale” pour plus d’informations sur SKEW (). L’idée de base est d’utiliser SKEW () pour calculer l’asymétrie de vos données transformées et pour que Solver trouve l’exposant qui amène le résultat de SKEW () le plus proche de zéro.

Visualisation de la population: statistiques inférentielles

L’autre raison générale pour examiner les distributions de fréquences est de faire une inférence à propos d’une population, en utilisant l’information que vous obtenez d’un échantillon comme base. C’est le domaine des statistiques inférentielles. Dans les chapitres suivants de ce cours, vous verrez comment utiliser les outils d’Excel
– en particulier, ses fonctions et ses graphiques – pour déduire les caractéristiques d’une population à partir de la distribution de fréquence d’un échantillon.
Un exemple familier est l’enquête politique. Lorsqu’un sondeur annonce que 53% des personnes interrogées préfèrent Smith, il rapporte une statistique descriptive. Cinquante-trois pour cent de l’échantillon ont préféré Smith, et aucune inférence n’est nécessaire.
Mais quand un autre sondeur rapporte que la marge d’erreur autour de cette statistique de 53% est de plus ou moins 3%, elle rapporte une statistique inférentielle. Elle extrapole de l’échantillon à la population plus large et déduit, avec un degré de confiance spécifié, qu’entre 50% et 56% de tous les électeurs préfèrent Smith.

La taille de la marge d’erreur rapportée, six points de pourcentage, dépend fortement de la confiance que le sondeur veut avoir. En général, plus vous faites confiance à votre extrapolation, plus la marge d’erreur que vous autorisez est grande. Si vous êtes sur un terrain de tir à l’arc et vous voulez être pratiquement certain de frapper votre cible, vous faites la cible aussi grande que nécessaire.

De même, si le sondeur veut être sûr à 99,9% de sa projection dans la population, la marge pourrait être si grande qu’elle serait inutile – disons plus ou moins 20%. Et bien qu’il ne soit pas question ici de signaler qu’entre 33% et 73% des électeurs préfèrent Smith, le sondeur peut être sûr que la projection est exacte.

Mais la taille de la marge d’erreur dépend également de certains aspects de la distribution de fréquence dans l’échantillon de la variable. Dans ce cas particulier (et relativement simple), l’exactitude de la projection de l’échantillon à la population dépend en partie du niveau de confiance souhaité (comme on vient de le dire brièvement), en partie de la taille de l’échantillon et en partie le pourcentage dans l’échantillon favorisant Smith. Les deux derniers problèmes, la taille de l’échantillon et le pourcentage en faveur, sont les deux aspects de la distribution de fréquence que vous déterminez en examinant les réponses de l’échantillon.

Bien sûr, ce n’est pas seulement les sondages politiques qui dépendent des distributions de fréquences inférences sur les populations. Voici quelques autres questions typiques posées par les chercheurs empiriques:
• Quel pourcentage des maisons existantes du pays ont été revendues au dernier trimestre?
• Quelle est l’incidence de la maladie cardiovasculaire aujourd’hui chez les diabétiques qui ont pris le médicament Avandia avant que des questions sur ses effets secondaires ne se posent en 2007? Cette incidence diffère-t-elle de façon fiable de l’incidence des maladies cardiovasculaires chez les personnes qui n’ont jamais pris le médicament?
• Un échantillon de 100 voitures fabriquées par un fabricant en particulier en 2016 avait une consommation d’essence moyenne de 26,5 mi / gal. Quelle est la probabilité que l’autoroute moyenne mpg, pour toutes les voitures de ce fabricant faites pendant cette année, est supérieure à 26,0 mpg?
• Votre entreprise fabrique de la verrerie personnalisée. Votre contrat avec un client ne nécessite pas plus de 2% d’articles défectueux dans un lot de production. Vous échantillonnez 100 unités de votre dernière production et en trouvez 5 qui sont défectueuses. Quelle est la probabilité que l’ensemble de la production de 1 000 unités ait un maximum de 20 unités défectueuses?

Dans chacun de ces quatre cas, les procédures statistiques spécifiques à utiliser – et donc les outils Excel spécifiques – seraient différentes. Mais l’approche de base serait la même: En utilisant les caractéristiques d’une distribution de fréquence à partir d’un échantillon, comparer l’échantillon à une population dont la distribution de fréquence est connue ou fondée dans un bon travail théorique. Utilisez les fonctions statistiques et autres fonctions numériques dans Excel pour estimer la probabilité que votre échantillon représente avec précision la population qui vous intéresse.