À ce stade, nous avons principalement parlé du concept de coefficient de corrélation – comment il est défini et comment il peut éclairer la nature de la relation entre deux variables. C’est une information utile en soi, mais les choses vont

beaucoup plus loin que cela. Par exemple, il vous est probablement venu à l’esprit que si vous connaissez la valeur d’une variable, vous pouvez prédire la valeur d’une autre variable corrélée avec la première.
Ce genre de prédiction est l’objet du reste de ce chapitre. Les bases discutées ici s’avèrent être le fondement de plusieurs analyses discutées dans les chapitres suivants. Utilisée de cette manière, la technique passe par le nom de régression, qui est la base de la désignation du coefficient de corrélation r.

Remarque
Pourquoi le mot régression? Au XIXe siècle, un scientifique et mathématicien nommé Francis Galton a étudié l’hérédité et a remarqué que des relations numériques existent entre les parents et les enfants, mesurées par certaines variables standards. Par exemple, Galton a comparé les hauteurs des pères aux hauteurs de leurs fils, et il est parvenu à une conclusion intéressante: les hauteurs des fils avaient tendance à être plus proches de leurs propres moyens que les hauteurs de leurs pères.
Autrement dit, les pères qui se tenaient, disons, deux écarts-types au-dessus de la hauteur moyenne de leur génération tendaient à avoir des fils dont la taille moyenne était juste un écart-type au-dessus de la taille moyenne de leur propre génération. De même, les pères qui étaient plus petits que la moyenne avaient tendance à avoir des fils qui étaient aussi plus petits que la moyenne, mais qui étaient plus proches de leur moyenne que leurs pères étaient à eux.

La taille des fils a régressé vers le moyen.
Les travaux ultérieurs de Karl Pearson, mentionnés plus haut dans ce chapitre, s’appuient sur le travail de Galton et développent les concepts et méthodes associés au coefficient de corrélation. La figure 4.13 montre quelques tailles de pères et de fils, et un graphique XY montrant visuellement comment les deux variables sont associées.
Figure 4.13. La ligne de régression montre où les points de données tomberaient si la corrélation était parfaite.

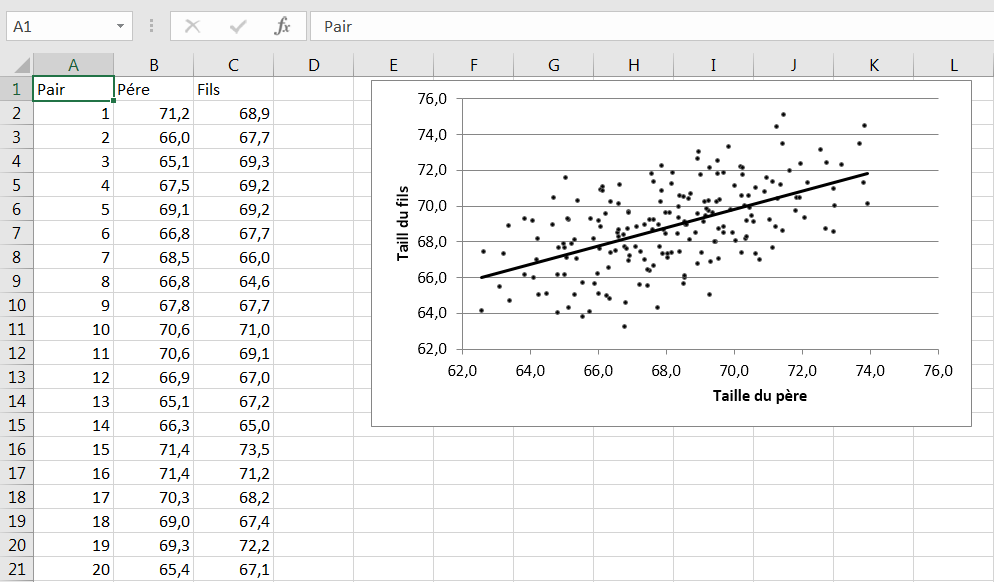
Étant donné que deux variables – ici, la taille du père et la taille du fils – sont corrélées, il devrait être possible de prédire une valeur d’une variable à partir d’une valeur de l’autre variable. Et c’est possible, mais l’accroc est que la prédiction ne sera parfaitement exacte que lorsque la relation est d’un intérêt très limité, comme la relation entre le poids en onces et le poids en grammes. La prédiction ne peut être parfaite que lorsque la corrélation est parfaite, et cela n’arrive que dans des situations hautement artificielles ou triviales.

La section suivante explique comment faire ce genre de prédiction sans compter sur Excel. Ensuite, je montre comment Excel le fait rapidement et facilement.