La figure 4.7 montre comment vous pourriez utiliser la fonction COEFFICIENT.CORRELATION()  pour examiner la relation entre deux variables qui vous intéressent. Supposons que vous êtes un agent de crédit dans une entreprise qui fournit des prêts

immobiliers, et vous voulez examiner la relation entre les prix d’achat et le revenu annuel des acheteurs pour les prêts que votre bureau a fait au cours du dernier mois.
Vous rassemblez les données nécessaires et entrez-les dans une feuille de calcul Excel comme indiqué dans les colonnes A à C de la Figure 4.7.
Figure 4.7. C’est toujours une bonne idée de valider la corrélation avec un graphique.

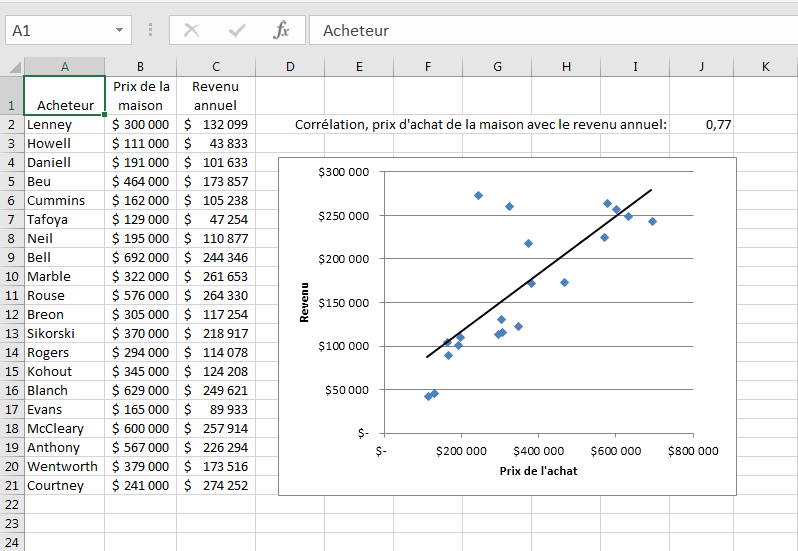
Notez dans la figure 4.7 qu’une valeur – ici, le nom de l’acheteur dans la colonne A – identifie de manière unique chaque paire de valeurs. Bien qu’un tel identificateur ne soit pas du tout nécessaire pour calculer un coefficient de corrélation, il peut être très utile de vérifier que les valeurs d’un enregistrement particulier sur les deux variables appartiennent réellement ensemble. Par exemple, sans le nom de l’acheteur dans la colonne A, il serait plus difficile de vérifier que la maison des Neils coûte 195 000 $ et que leur revenu annuel est de 110 877 $. Si vous n’avez pas les valeurs sur une variable appariée avec les valeurs appropriées sur l’autre variable, le coefficient de corrélation ne sera calculé correctement que par accident. Par conséquent, il est bon de s’assurer que, par exemple, le revenu de 110 877 $ des Neils correspond au coût de 195 000 $.

Remarque
Formellement, la seule restriction est que deux mesures du même enregistrement occupent la même position relative dans les deux tableaux, comme indiqué précédemment dans “La corrélation, calculée”. Je recommande que chaque valeur pour un enregistrement donné occupe la même rangée car cela fait les données sont plus faciles à valider et parce que vous voulez souvent utiliser COEFFICIENT.CORRELATION()  avec les colonnes d’une liste ou d’une table comme arguments. Les listes et les tables fonctionnent correctement uniquement si chaque valeur d’un enregistrement donné est sur la même ligne.
Vous obtiendrez facilement la corrélation entre le prix du logement et le revenu dans l’échantillon actuel. Entrez simplement la formule suivante dans une cellule de feuille de calcul, comme indiqué dans la cellule J2 de la figure 47:
= COEFFICIENT.CORRELATION (B2: B21, C2: C21)
Obtenir simplement la corrélation n’est pas la fin du travail, cependant. Les coefficients de corrélation peuvent être difficiles. Voici deux façons dont ils peuvent vous diriger mal:
• Il existe une relation forte entre les deux variables, mais le coefficient de corrélation normal, r, obscurcit cette relation.

• Il n’y a pas de relation forte entre les deux variables, mais une ou deux observations très inhabituelles donnent l’impression qu’il y en a une.
La figure 4.8 montre un exemple de relation forte que r ne vous dit pas.
Si vous deviez simplement calculer le coefficient de corrélation de Pearson  ou standard au moyen de COEFFICIENT.CORRELATION()  sur les données utilisées pour la figure 4.8, vous ne pourriez pas savoir ce qui se passe. Le théorème de Pearson suppose que la relation entre les deux variables est linéaire, c’est-à-dire qu’elle calcule une droite de régression droite, comme le montre la figure 4.7. La figure 4.8 montre les résultats que vous pourriez obtenir si vous établissiez l’âge en fonction du nombre d’erreurs typographiques par 1 000 mots. Les personnes très jeunes dont la coordination oeil-main est en cours de développement ont tendance à faire plus d’erreurs, tout comme celles des années suivantes, car leur acuité visuelle commence à diminuer.

Figure 4.8. La relation n’est pas linéaire et r suppose des relations linéaires.
 

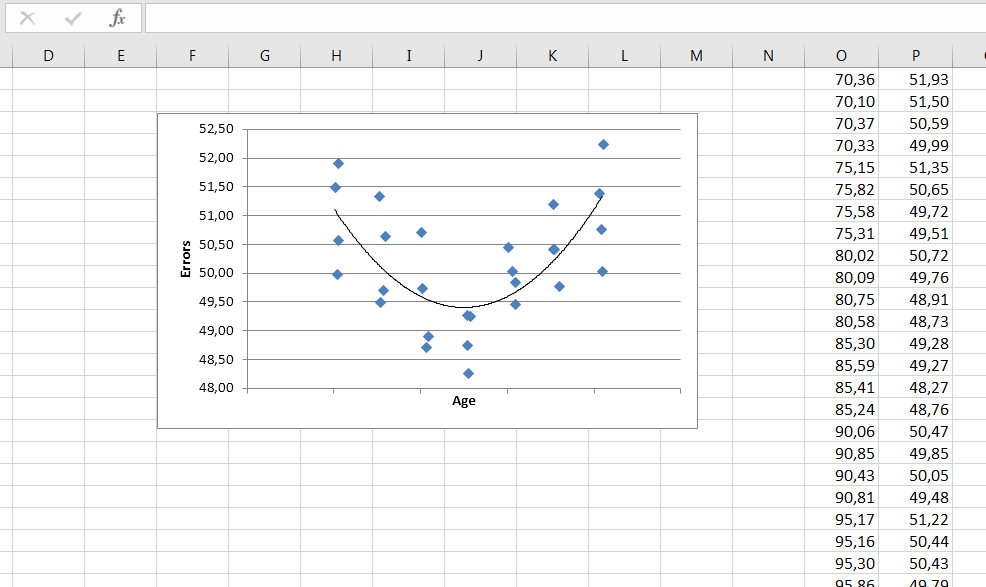
Une mesure de la corrélation non linéaire indique qu’il existe une corrélation de 0,75 entre les variables. Mais COEFFICIENT.CORRELATION() calcule le r de Pearson à 0,08 parce que cette fonction n’est pas conçue pour prendre en compte une relation non linéaire. Vous pourriez manquer un résultat important si vous n’avez pas cartographié les données. Un problème différent apparaît dans la Figure 4.9.
Figure 4.9. Une seule valeur aberrante peut surestimer la relation entre les variables.

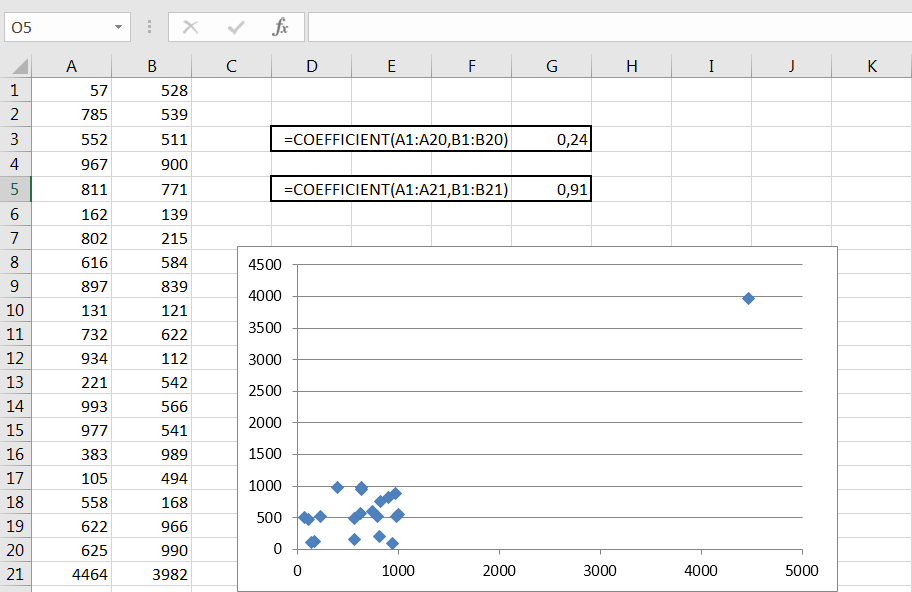Dans la Figure 4.9, deux variables faiblement reliées sont montrées dans les cellules A1: B20 (oui, B20, pas B21). La corrélation entre eux est montrée dans la cellule G3: Elle est seulement .24.
D’une manière ou d’une autre, à cause d’une faute de frappe ou de lectures incorrectes sur les compteurs ou d’une requête de base de données mal structurée, deux valeurs supplémentaires apparaissent dans les cellules A21: B21. Lorsque ces deux valeurs sont incluses dans les arguments de la fonction COEFFICIENT.CORRELATION(), la corrélation passe d’un faible 0.24 à un fort 0.91.

Cela arrive à cause de la façon dont la covariance, et donc la corrélation, est définie. Passons en revue une formule de covariance donnée plus tôt, utilisée avec un ensemble d’observations qui constituent un échantillon :

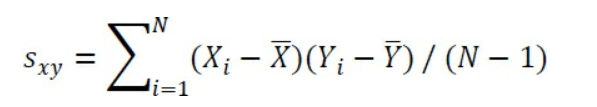
L’expression dans le numérateur multiplie l’écart d’observation de la moyenne de X fois l’écart de l’observation par rapport à la moyenne de Y. L’addition de cet enregistrement, où les valeurs X et Y s’écartent de milliers d’unités des moyennes des deux variables, gonfle la covariance, et donc la corrélation, bien au-dessus de leurs valeurs basées sur les 20 premiers enregistrements.
Vous n’avez peut-être pas réalisé ce qui se passait sans le tableau XY qui l’accompagne. Là, vous pouvez voir la seule observation qui transforme ce qui n’est fondamentalement pas de relation en un fort. Bien sûr, il est possible que la seule aberration soit entièrement légitime. Mais dans ce cas, il se peut que le coefficient de corrélation standard ne soit pas une expression appropriée de la relation entre les deux variables (pas plus que la moyenne est une expression appropriée de la tendance centrale dans une distribution fortement asymétrique).
Prenez l’habitude de créer des diagrammes XY de variables que vous étudiez via l’analyse de corrélation. La norme r, le coefficient de corrélation de Pearson, est à la base de nombreuses analyses statistiques sophistiquées, mais elle n’a pas été conçue pour évaluer la force des relations qui sont non linéaires ou qui contiennent des valeurs aberrantes extrêmes.
Heureusement, Excel rend très facile la création des graphiques. Par exemple, pour créer le graphique XY illustré à la Figure 4.9, procédez comme suit:
1. Avec les données brutes comme indiqué dans les cellules A1: B21, sélectionnez n’importe quelle cellule dans cette plage.
2. Cliquez sur l’onglet Insérer du ruban.
3. Cliquez sur le bouton Insérer une dispersion (X, Y) ou un graphique à bulles dans le groupe Graphes.
4. Cliquez sur le type dispersion dans la liste déroulante.