Je vous ai infligé tout cela parce que cela aide à éclairer la relation entre les scores bruts et les covariances, entre les z-scores et les corrélations. Comme vous pouvez vous y attendre, Excel vous soulage de l’ennui de faire tout ce que la main

formule ondulante.
La figure 4.15 montre les données brutes et certains calculs préliminaires sur lesquels la discussion précédente était basée.
Figure 4.15. La fonction TENDANCE () prend en charge tous les calculs pour vous.
 

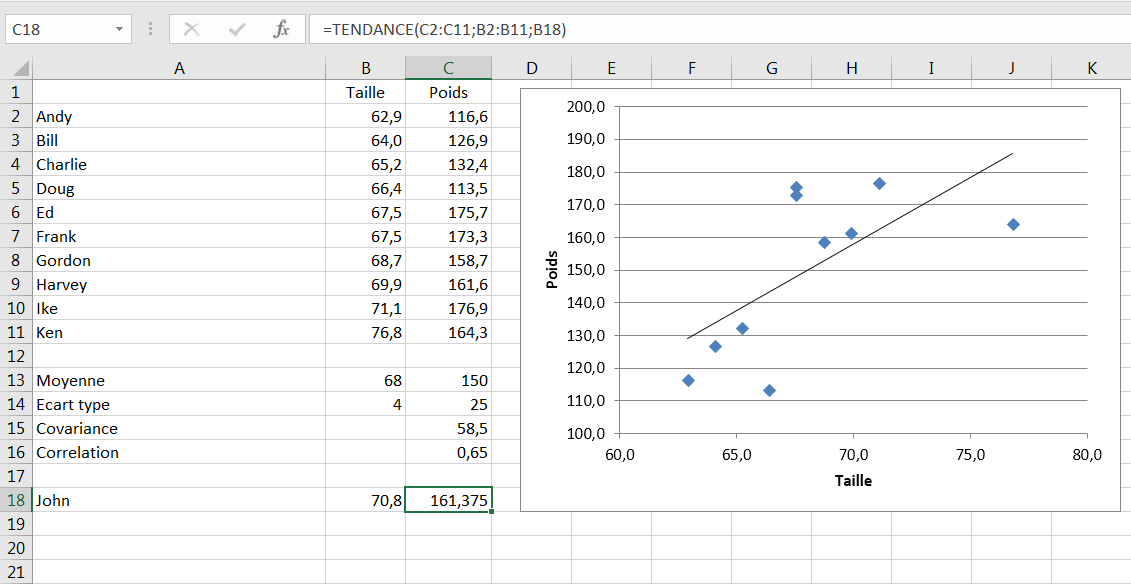
Pour prédire le poids de John en utilisant les données illustrées aux Figures 4.14 et 4.15, entrez cette formule dans une cellule vide (C18 dans la Figure 4.15):
= TENDANCE (C2: C11, B2: B11, B18)
Avec cet ensemble de données, la formule renvoie la valeur 161.375. Pour obtenir la même valeur en utilisant la méthode panoramique de la Figure 4.14, vous pouvez également entrer la formule
= ((B18-B13) / B14) * C16 * C14 + C13
qui effectue les calculs qui ont été esquissés dans la section précédente : Calculer le z-score de John pour la taille, multipliez-le par la corrélation, multipliez-le par l’écart-type pour le poids et ajoutez le poids moyen. Heureusement, la fonction TENDANCE () vous aide à éviter toutes ces occasions de faire une erreur.
La syntaxe de la fonction TENDANCE est la suivante :
= TENDANCE (known_y’s, known _x’s, new_x’s, const)
Remarque
Le quatrième argument, const, est facultatif.

Les trois premiers arguments à TENDANCE () sont discutés par la suite.

known_y’s
Ce sont les valeurs que vous avez déjà en main pour la variable que vous voulez prédire. Dans l’exemple de la section précédente, cette variable est le poids: l’idée était de prédire le poids de John sur la base de la corrélation entre la taille et le poids, combinée à la connaissance de la taille de John. Il est conventionnel en écriture statistique de désigner la variable prédite par Y, et ses valeurs individuelles par y.
known_x’s
Ce sont les valeurs de la variable que vous voulez prédire. Chacun doit être jumelé avec l’un des known_y. Vous constaterez que la façon la plus simple de faire cela est d’aligner deux plages adjacentes comme dans la Figure 4.15, où les x connus sont dans B2: B11 et ceux connus dans C2: C11.
new_x’s
Cette valeur appartient à la variable prédictive, mais vous n’avez pas ou ne fournissez pas de valeurs associées pour la variable prédite. Il y a plusieurs raisons pour lesquelles vous pourriez avoir new_x à utiliser comme argument pour TENDANCE (), mais la raison typique est que vous voulez prédire y pour les new_x, basé sur la relation entre les known_y et les known_x. Par exemple, les notations_x peuvent être des années: 1980, 1981, 1982, etc. Le know_y peut être le revenu de l’entreprise pour chacune de ces années. Et votre new_x pourrait être le numéro de l’année prochaine, tel que 2019, pour lequel vous souhaitez prédire les revenus.

Obtenir les valeurs prévues
Si vous n’avez qu’une seule valeur new_x à prédire, vous pouvez entrer la formule avec la fonction TENDANCE () simplement en la tapant et en appuyant sur Entrée. C’est la situation de la figure 4.15, où vous devez entrer = TENDANCE (C2: C11, B2: B11, B18) dans une cellule vide telle que C18 pour obtenir le poids prévu compte tenu de la Taille dans B18.
Mais supposons que vous vouliez savoir quel serait le poids prévu de tous les sujets de votre échantillon, étant donné la corrélation entre les deux variables. TENDANCE () le fait aussi pour vous: vous avez simplement besoin d’entrer dans la table.
Vous commencez par sélectionner une plage de cellules ayant les mêmes dimensions que celles de votre fichier known_x. Dans la figure 4.15, les x connus sont dans B2: B11, vous pouvez donc sélectionner D2: D11. Tapez ensuite la formule = TENDANCE (C2: C11, B2: B11) et ensuite Ctrl + Shift + Entrer au lieu de simplement entrer.

Remarque
Les formules de tableau sont discutées plus en détail dans le chapitre 2, dans la section intitulée «Utilisation d’une formule de tableau pour compter les valeurs».
Le résultat apparaît sur la Figure 4.16.
Figure 4.16. Les accolades autour de la formule dans la boîte de formule indiquent qu’il s’agit d’une formule matricielle.

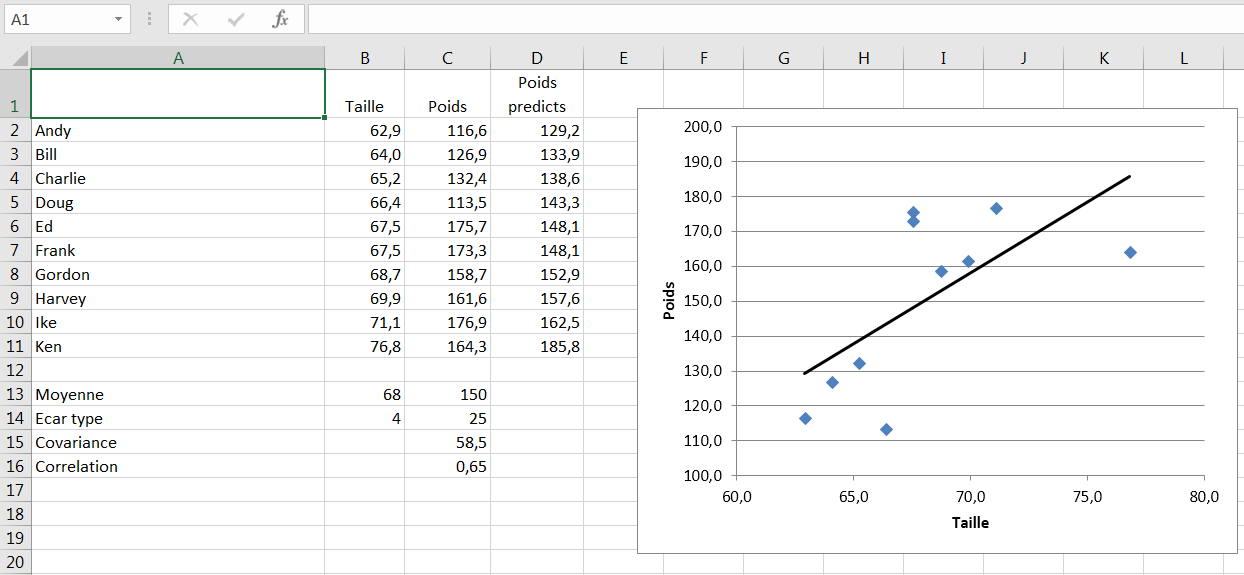
Vous pouvez mieux comprendre la signification de la courbe de tendance dans le graphique si vous utilisez les valeurs prédites dans D2: D11 de la Figure 4.16. Si vous créez un graphique XY en utilisant les valeurs de B2: B11 et D2: D11, vous verrez que vous avez un graphique qui duplique la courbe de tendance dans le graphique de la figure 4.16.
Ainsi, une ligne de tendance linéaire dans un graphique représente la situation irréaliste dans laquelle toutes les observations suivent docilement une formule qui relie deux variables. Mais Ed mange trop et Doug ne mange pas assez. Ils, avec le reste des sujets, s’éloignent dans une certaine mesure de la ligne de tendance parfaite.
Si c’est irréaliste, à quoi sert d’inclure une ligne de tendance dans un graphique ? Il s’agit en grande partie de vous aider à visualiser à quel point les observations individuelles tombent de la formule mathématique. Plus les écarts sont importants, plus la corrélation est faible.