■■ Quelles sont les propriétés de la variable aléatoire normale?

■■ Comment puis-je utiliser Excel pour trouver des probabilités pour la variable aléatoire normale?

■■ Puis-je utiliser Excel pour trouver des centiles pour des variables aléatoires normales?

■■ Pourquoi la variable aléatoire normale est-elle appropriée dans de nombreuses situations du monde réel?

Réponses aux questions de cet article

Cette section fournit les réponses aux questions répertoriées au début de cet article.

Quelles sont les propriétés de la variable aléatoire normale?

Au chapitre 66, «Introduction aux variables aléatoires», vous avez appris que des variables aléatoires continues peuvent être utilisées pour modéliser des quantités telles que les suivantes:

■■ Prix des actions Microsoft dans un an

■■ Part de marché pour un nouveau produit

■■ Taille du marché pour un nouveau produit

■■ Coût de développement d’un nouveau produit

■■ Poids du nouveau-né

■■ Le QI d’une personne

N’oubliez pas que si une variable aléatoire discrète (comme les ventes de Big Mac en 2014) peut prendre de nombreuses valeurs possibles, vous pouvez approximer la valeur en utilisant également une variable aléatoire continue. Comme décrit au chapitre 66, toute variable aléatoire continue X a une fonction de densité de probabilité (pdf). Le pdf pour une variable aléatoire continue est une fonction non négative avec les propriétés suivantes (a et b sont des nombres arbitraires):

■■ La zone sous le pdf est 1.

■■ La probabilité que X <a soit égale à la probabilité que X ≤ a. Cette probabilité est représentée par l’aire sous le pdf à gauche de a.

683

■■ La probabilité que X> b soit égale à la probabilité que X ≥ b. Cette probabilité est indiquée dans la zone sous le pdf à droite de b.

■■ La probabilité que a <X <b soit égale à la probabilité que a ≤ X ≤ b. Cette probabilité est l’aire sous le pdf entre a et b.

Ainsi, l’aire sous le pdf d’une variable aléatoire continue représente la probabilité. De plus, plus la valeur de la fonction de densité en X est grande, plus la variable aléatoire prendra probablement une valeur proche de X. Par exemple, si la fonction de densité d’une variable aléatoire à 20 est deux fois la fonction de densité de la variable aléatoire à 5, alors la variable aléatoire est deux fois plus susceptible de prendre une valeur proche de 20 qu’une valeur proche de 5.

Pour une variable aléatoire continue, la probabilité que X soit égal à n’importe quelle valeur sera toujours égale à 0. Par exemple, certaines personnes mesurent de 5,99999 pieds à 6,00001 pieds, mais personne ne peut être exactement 6 pieds de haut. Cela explique pourquoi vous pouvez remplacer le signe inférieur à (<) par le signe inférieur ou égal à (≤) dans les énoncés de probabilité.

La figure 1 affiche le pdf pour X = IQ d’une personne choisie au hasard. L’aire sous ce pdf est 1. Si vous voulez trouver la probabilité que le QI d’une personne soit inférieur ou égal à 90, vous trouvez simplement l’aire à gauche de 90. Si vous voulez trouver la probabilité que le QI d’une personne soit de 95 à 120, vous trouvez l’aire sous le pdf de 95 à 120. Si vous voulez trouver la probabilité que le QI d’une personne soit supérieur à 130, vous trouvez l’aire sous la fonction de densité à droite de 130. (Voir la Feuille de calcul Densité IQ dans le fichier .)

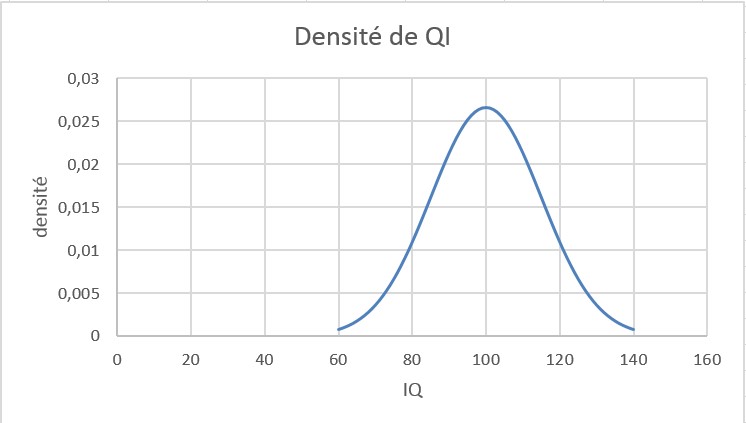
FIGURE 1 IQ pdf.

En fait, la densité représentée sur la figure 1 est un exemple de la variable aléatoire normale. La variable aléatoire normale est spécifiée par sa moyenne et son écart-type. Les QI suivent une variable aléatoire normale avec µ = 100 et σ = 15. Il s’agit du pdf affiché dans la figure 1. La variable aléatoire normale a les propriétés suivantes:

■■ La valeur la plus probable d’une variable aléatoire normale est µ (comme indiqué par le pdf avec un pic à 100 dans la figure 1).

■■ Lorsque la valeur x de la variable aléatoire s’éloigne de µ, la probabilité que la variable aléatoire soit proche de x diminue fortement.

■■ La variable aléatoire normale est symétrique par rapport à sa moyenne. Par exemple, des QI proches de 80 sont aussi probables que des QI proches de 120.

■■ Une variable aléatoire normale a 68% de sa probabilité à σ de sa moyenne, 95% à 2σ de sa moyenne et 99,7% à 3σ de sa moyenne. Ces mesures devraient vous rappeler la règle générale décrite au chapitre 42, «Synthèse des données à l’aide de statistiques descriptives». En fait, la règle empirique est basée sur l’hypothèse que les données sont échantillonnées à partir d’une distribution normale, ce qui explique pourquoi la règle empirique ne fonctionne pas aussi bien lorsque les données ne présentent pas d’histogramme symétrique.

Pour un σ plus grand, une variable aléatoire normale est plus étalée sur sa moyenne. Ce schéma est illustré et  représenté dans les  figures 2 et 3. (Voir la feuille de calcul Sigma de 5 et 15 dans le fichier )

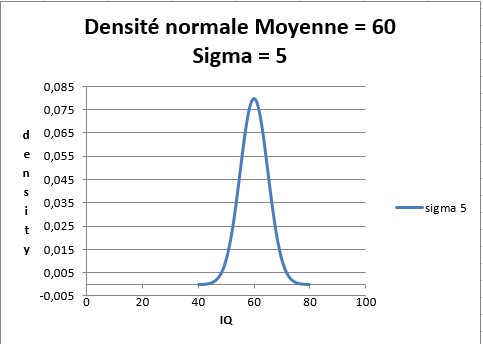
FIGURE 2 Variable aléatoire normale pdf avec une moyenne égale à 60 et un écart type égal à 5.

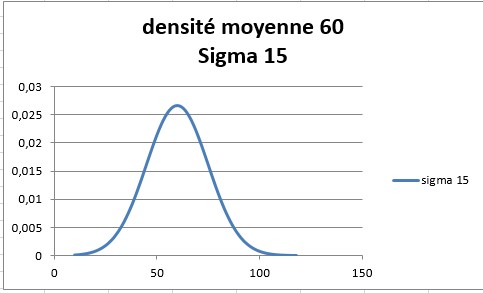
FIGURE 3 Variable aléatoire normale pdf avec une moyenne égale à 60 et un écart-type égal à 15.

Comment puis-je utiliser Excel pour trouver des probabilités pour la variable aléatoire normale?

Considérons une variable aléatoire normale X avec une moyenne µ et un écart type σ. Supposons que pour tout nombre- b  et x, vous voulez trouver la probabilité que X ≤ x, qui est appelée la fonction cumulative normale. Pour utiliser Microsoft Excel 2013 pour trouver la probabilité que X ≤ x, entrez la formule LOI.NORMALE.STANDARD (x, µ, σ, 1). Bien sûr, le quatrième argument de 1 pourrait être remplacé par Vrai.

L’argument 1 indique à Excel de calculer le cumul normal. Si le dernier argument de la fonction est 0, Excel renvoie la valeur réelle de la variable aléatoire normale pdf. Les fonctions statistiques d’Excel 2013 (telles que LOI.NORMALE.STANDARD) ont été entièrement modifiées ou repensées pour offrir une meilleure précision que leurs homologues (telles que LOI.NORMALE.STANDARD) dans les versions précédentes d’Excel.

Vous pouvez utiliser la fonction LOI.NORMALE.STANDARD pour répondre à de nombreuses questions concernant les probabilités normales. Vous pouvez trouver des exemples dans la feuille de calcul Normal du fichier, qui est illustré à la figure 4 et dans les trois scénarios suivants.

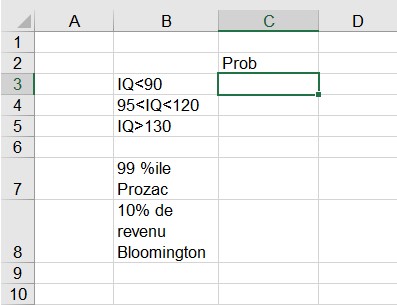
FIGURE 4 Calcul de la probabilité normale.

■■ Quelle fraction des personnes a un QI inférieur à 90? Soit X égal au QI d’une personne choisie au hasard. Ensuite, vous recherchez la probabilité que X <90, qui est égale à la probabilité que X ≤ 90. Par conséquent, vous pouvez entrer la formule NORM.DIST (90,100,15,1) dans la cellule C3 de la feuille de calcul Normal et Excel renvoie 0,252 . Ainsi, 25,2% de toutes les personnes ont un QI inférieur à 90.

■■ Quelle fraction de toutes les personnes a un QI de 95 à 120? Pour trouver la probabilité que a ≤ X ≤ b, vous utilisez la formule (aire sous la fonction de densité normale à gauche de b) – (aire sous la fonction de densité normale à gauche de a). Ainsi, vous pouvez trouver la probabilité que a ≤ X ≤ b en entrant la formule LOI.NORMALE.STANDARD (b, µ, s, 1) – LOI.NORMALE.STANDARD (a, µ, s, 1). Vous pouvez répondre à la question sur les QI de 95 à 120 en entrant la formule LOI.NORMALE.STANDARD (120,100,15,1) – LOI.NORMALE.STANDARD (95,100,15,1) dans la cellule C4 de la feuille de calcul Normal. Excel renvoie la probabilité 0,539, de sorte que 53,9% de toutes les personnes ont un QI compris entre 95 et 120.

■■ Quelle fraction de toutes les personnes a un QI d’au moins 130? Pour trouver la probabilité que X ≥ b, notez que la probabilité que X ≥ b soit égal à 1 – probabilité X <b. Vous pouvez calculer la probabilité que X ≥ b en entrant la formule 1 – LOI.NORMALE.STANDARD (b, µ, σ, 1). Vous recherchez la probabilité que X ≥ 130. Cela équivaut à 1 – la probabilité X <130. Vous entrez le 1 – LOI.NORMALE.STANDARD (130,100,15,1) formule dans la cellule C5 de la feuille de calcul Normal. Excel renvoie 0,023, vous savez donc que 2,3% des personnes ont un QI d’au moins 130.

Puis-je utiliser Excel pour trouver des centiles pour des variables aléatoires normales?

Considérons une variable aléatoire normale X donnée avec la moyenne et l’écart type. Dans de nombreuses situations, vous souhaitez répondre à des questions telles que les suivantes:

■■ Un fabricant de médicaments estime que la demande de l’année prochaine pour son antidépresseur populaire sera normalement distribuée, avec une moyenne égale à 60 millions de jours de thérapie (DOT) et un sigma égal à 5 millions de DOT. Combien d’unités de médicament devraient être produites cette année si l’entreprise veut avoir seulement 1% de chance de manquer de médicament?

■■ Le revenu familial à Bloomington, Indiana, est normalement distribué, avec une moyenne égale à 30 000 $ et sigma égale à 8 000 $. Les 10% les plus pauvres de toutes les familles de Bloomington sont éligibles à l’aide fédérale. Quelle devrait être la coupure de l’aide?

Dans le premier exemple, vous voulez déterminer le quatre-vingt-dix-neuvième centile de la demande d’antidépresseur. Autrement dit, vous recherchez le nombre x de telle sorte qu’il y ait seulement 1% de chance que la demande dépasse x et 99% de chance que la demande soit inférieure à x. Dans le deuxième exemple, vous voulez le dixième centile du revenu familial à Bloomington. Autrement dit, vous recherchez le nombre x de telle sorte qu’il y ait seulement 10% de chances que le revenu familial soit inférieur à x et 90% de chances que le revenu familial dépasse x.

Supposons que vous vouliez trouver le pième percentile (exprimé sous forme décimale) d’une variable aléatoire normale X avec une moyenne et un écart-type. Dans Excel , entrez simplement la formule LOI.NORMALE.INVERSE.N (p, µ, σ). Cette formule renvoie un nombre x tel que la probabilité que X ≤ x soit égal au pourcentage spécifié utille. Vous pouvez maintenant résoudre vos exemples. Vous trouverez ces exercices sur la feuille de calcul Normal dans le Fichier.

Pour l’exemple de fabrication du médicament, soit X une demande annuelle égale pour le médicament. Vous voulez une valeur x telle que la probabilité que X ≥ x soit égal à 0,01 ou la probabilité que X <x soit égal à 0,99. Encore une fois, vous recherchez le quatre-vingt-dix-neuvième centile de la demande, que vous trouvez (en millions) en entrant dans la  Formule LOI.NORMALE.INVERSE.N (0.99,60,5) dans la cellule C7. Excel renvoie 71,63, la société doit donc produire 71 630 000 DOT. Cela suppose, bien sûr, que la société commence l’année sans approvisionnement en médicament. Si, par exemple, elle avait un stock initial de 10 millions de DOT, elle devrait produire 61 630 000 DOT au cours de l’année en cours.

Pour déterminer le seuil de l’aide fédérale, si X est égal au revenu d’une famille Bloomington, vous recherchez une valeur de x telle que la probabilité que X ≤ x soit 0,10, ou le dixième centile de Bloomington revenu familial. Vous trouvez cette valeur avec la formule LOI.NORMALE.INVERSE.N (0.10,30000,8000). Retours Excel 19 747,59 $, donc une aide devrait être accordée à toutes les familles dont le revenu est inférieur à 19 749,59 $.

Pourquoi la variable aléatoire normale est-elle appropriée dans de nombreuses situations du monde réel?

Un résultat mathématique bien connu appelé le théorème central limite indique que si vous additionnez de nombreuses variables aléatoires indépendantes (généralement au moins 30 suffisent), leur somme est normalement distribuée. Ce résultat est vrai même si les variables aléatoires individuelles ne sont pas normalement distribuées. Beaucoup les quantités (telles que les erreurs de mesure) sont créées en additionnant de nombreuses variables aléatoires indépendantes, ce qui explique pourquoi la variable aléatoire normale se produit souvent dans le monde réel. Voici quelques autres situations dans lesquelles vous pouvez utiliser le théorème de la limite centrale:

■■ La demande totale de pizzas pendant un mois dans un supermarché est normalement répartie même si la demande quotidienne de pizzas ne l’est pas.

■■ Le montant d’argent que vous gagnez si vous jouez au craps 1 000 fois est normalement distribué, même si le montant d’argent que vous gagnez sur chaque jeu individuel ne l’est pas.

Un autre résultat mathématique important montre comment trouver la moyenne, la variance et les écarts-types des sommes de variables aléatoires indépendantes . Si vous additionnez des variables aléatoires indépendantes  où la moyenne , et l’écart-type , alors ce qui suit est vrai:

1. 1. Moyenne
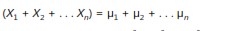
2. 2. Variance
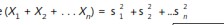
3. 3. Écart type

Notez que 1 est vrai même lorsque les variables aléatoires ne sont pas indépendantes. En combinant 1 à 3 avec le théorème central limite, vous pouvez résoudre de nombreux problèmes de probabilité complexes, tels que les suivants: Supposons que la demande quotidienne de pizza ne soit pas normalement distribuée mais ait une moyenne de 45 et un sigma de 10. Quelle est la probabilité qu’au moins 1 400 pizzas soient vendues au cours d’un mois? Votre solution pizza se trouve dans la feuille de calcul Central Limit du fichier, qui est illustré à la figure 5.

FIGURE 5 Utilisation du théorème de la limite centrale.

Même si la demande quotidienne de pizzas surgelées n’est pas normalement distribuée, vous savez d’après le théorème de la limite centrale que la demande de 30 jours de pizzas surgelées est normalement distribuée. Compte tenu de cela, les 1 à 3 précédents impliquent ce qui suit:

■■ À partir de 1, la moyenne d’une demande sur 30 jours est égale à 30 (45) = 1 350.

■■ À partir de 2, la variance d’une demande sur 30 jours est égale à 30 (12) 2 = 4 320.

■■ À partir de 3, l’écart-type d’une demande à 30 jours est égal à 65,73.

Ainsi, la demande de pizzas sur 30 jours peut être modélisée selon une variable aléatoire normale avec une moyenne de 1 350 et un écart-type de 65,73. Dans la cellule D11, la probabilité qu’au moins 1 400 pizzas soient vendues est calculée comme la probabilité que l’approximation normale soit au moins 1 399,5.

(notez qu’une demande de 1 399,6, par exemple, arrondirait à 1 400) avec le 1 –

Formule LOI.NORMALE.N (1399.5, D7, D9, VRAI). Vous trouvez la probabilité que la demande dans une période de 30 jours pour au moins au moins 1 400 pizzas représentent 22,6%.

Le nombre de pizzas que vous devez stocker pour avoir seulement 1% de chances de manquer de pizzas n’est que le quatre-vingt-dix-neuvième centile de la distribution de la demande. Vous déterminez le quatre-vingt-dix-neuvième pour cent de la distribution de la demande (1 503) dans la cellule D12 avec la formule LOI.NORMALE.N (0.99, D7, D9). Par conséquent, au début d’un mois, vous devriez porter votre stock de pizzas à 1 503 si vous voulez avoir seulement 1% de chance de manquer de pizzas.