Vous utilisez normalement le mot paramètre pour un nombre qui décrit une population et le mot statistique pour un nombre qui décrit un échantillon. Donc, la moyenne d’une population est un paramètre, et la moyenne d’un échantillon est une

statistique.
Ce cours essaie d’éviter d’utiliser des symboles lorsque cela est possible, mais vous les rencontrerez tôt ou tard. L’un des endroits où vous les trouverez est la documentation d’Excel. Il est classique d’utiliser des lettres grecques pour les paramètres qui décrivent une population et d’utiliser des lettres romaines pour les statistiques qui décrivent un échantillon.

Compte tenu de ces conventions – c’est-à-dire les lettres grecques pour représenter les paramètres de population et les lettres romaines pour représenter les statistiques de l’échantillon – l’équation qui définit la variance pour un échantillon donné ci-dessus devrait être différente pour la variance d’une population. La variance en tant que paramètre est définie de cette manière:

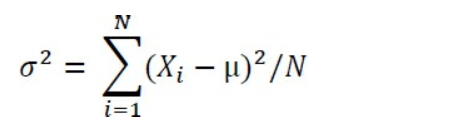
L’équation présentée ici est fonctionnellement identique à l’équation de la variance de l’échantillon donnée précédemment. Cette équation utilise le grec minuscule, sigma prononcé.

Remarque
La dernière équation utilise également le sigma majuscule. Ce n’est ni une statistique ni un paramètre, mais un opérateur, un peu comme un signe plus ou moins. Cela signifie simplement “retourner la somme de toutes les valeurs qui suivent ce symbole”. Dans ce cas, c’est la somme de tous les écarts quadratiques par rapport à la moyenne.

Division par N – 1
Une autre question concerne la formule qui calcule la variance (et donc l’écart-type). Il reste impliqué lorsque vous voulez estimer la variance d’une population au moyen de la variance d’un échantillon de cette population. Si vous vous demandiez pourquoi le chapitre 2 est allé à de telles longueurs pour discuter de la moyenne en termes de minimisation de la somme des écarts au carré, vous trouverez une raison majeure dans cette section.
Rappelons du chapitre 2 cette propriété de la moyenne: Si vous calculez l’écart de chaque valeur d’un échantillon par rapport à la moyenne de l’échantillon, ajustez les écarts et totalisez-les, le résultat est plus petit que si vous utilisez la moyenne. Vous pouvez trouver ce concept longuement discuté dans la section du chapitre 2 intitulée «Minimiser la propagation».

Supposons maintenant que vous ayez un échantillon de 100 segments de piston provenant d’une population de 10 000 anneaux, par exemple, que votre entreprise a fabriquée. Vous avez une mesure du diamètre de chaque anneau dans votre échantillon, et vous calculez la variance des anneaux en utilisant la formule de définition:

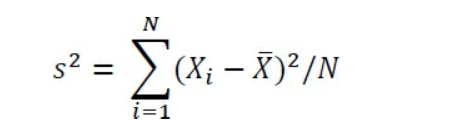
Vous obtiendrez une valeur précise de la variance dans l’échantillon, mais cette valeur est susceptible de sous-estimer la variance dans la population de 10 000 anneaux. À son tour, si vous prenez la racine carrée de la variance pour obtenir l’écart-type en tant qu’estimation de l’écart-type de la population, la sous-estimation vient pour le tour.
Si vous calculez l’âge moyen de 10 personnes dans une classe de 30 élèves, il est presque certain que l’âge moyen de l’échantillon de 10 élèves sera différent, même légèrement, de l’âge moyen des 30 élèves de la classe.

De même, il est très probable que le diamètre moyen du segment de piston de votre échantillon soit différent, même légèrement, du diamètre moyen de votre population de 10 000 segments de piston. La moyenne de votre échantillon est calculée sur la base des 100 anneaux de votre échantillon. Par conséquent, le résultat du calcul

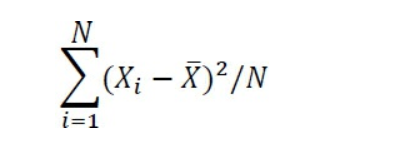
qui utilise la moyenne de l’échantillon est différente et plus petite que le résultat du calcul

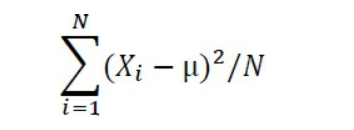
qui utilise la moyenne de la population (D’après le résultat est démontré au chapitre 2).
Gardez à l’esprit que lorsque vous calculez les écarts en utilisant la moyenne des observations de l’échantillon, vous minimisez la somme des écarts quadratiques par rapport à la moyenne de l’échantillon. Si vous utilisez un autre nombre, tel que la moyenne de la population, le résultat sera différent et sera plus grand que le résultat lorsque vous utiliserez la moyenne de l’échantillon.

Par conséquent, chaque fois que vous estimez la variance (ou l’écart-type) d’une population à l’aide de la variance (ou de l’écart-type) d’un échantillon, il est pratiquement certain que votre statistique sous-estimera le paramètre population.
Il n’y aurait pas de problème si la moyenne de votre échantillon était la même que la moyenne de la population, mais c’est une situation très improbable.
Y a-t-il un facteur de correction qui peut être utilisé pour compenser la sous-estimation? Oui il y en a un . Vous utiliseriez cette formule pour calculer avec précision la variance d’un échantillon:

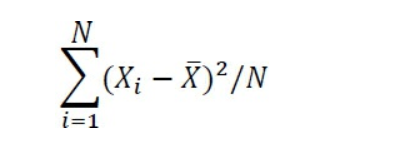
Mais si vous voulez estimer la valeur de la variance de la population à partir de laquelle vous avez prélevé votre échantillon, vous divisez par N – 1 pour arriver à cette estimation:
  

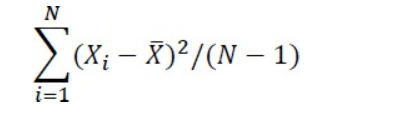
La quantité (N – 1) dans cette formule est appelée les degrés de liberté.
De même, cette formule est la formule utilisée pour estimer l’écart type d’une population sur la base des observations d’un échantillon (c’est juste la racine carrée de l’estimation de la variance de la population):
 

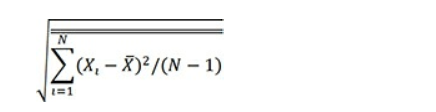
Si vous regardez dans la documentation pour les fonctions de variance d’Excel, vous verrez que VAR () ou, dans Excel 2010 à 2016, VAR.S () est recommandé si vous voulez estimer une variance de population à partir d’un échantillon. Ces fonctions utilisent les degrés de liberté dans leurs dénominateurs.
Les fonctions VARP () et, dans Excel 2010 à 2016, VAR.PEARSON () sont recommandées si vous calculez la variance d’une population en fournissant les valeurs de la population entière comme argument de la fonction. De façon équivalente, si vous avez un échantillon d’une population, mais n’avez pas l’intention de déduire une variance de population – vous voulez simplement connaître la variance de l’échantillon ou si vous considérez l’échantillon comme une population – vous utiliseriez VARP () ou VAR .PEARSON (). Ces fonctions utilisent N, pas les N – 1 degrés de liberté, dans leurs dénominateurs.
La même chose est vraie pour ECARTYPE.PEARSON (). Utilisez-les pour obtenir l’écart type d’une population ou d’un échantillon lorsque vous n’avez pas l’intention de déduire l’écart-type de la population.
Utilisez ECARTYPE () ou ECARTYPE.STANDARD () pour déduire l’écart type d’une population à partir d’un échantillon d’observations. Les fonctions ECARTYPE.STANDARD ( ) et ECARTYPE.PEARSON ( ) sont disponibles dans Excel de 2010 à 2016.